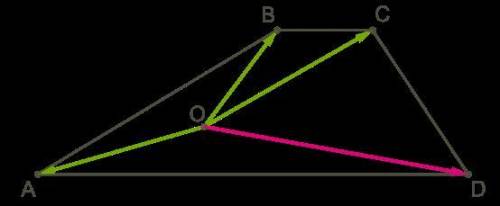
Дана трапеция ABCD, у которой AD = 8BC. Вырази вектор OD−→− через векторы OA−→−, OB−→− и OC−→−.

OD−→−=

⋅OA−→−−

⋅OB−→−+

⋅OC−→−.

Для того чтобы выразить вектор OD−→− через векторы OA−→−, OB−→− и OC−→−, следует воспользоваться свойствами векторов.

Обратимся к теореме о прилежащих углах в трапеции ABCD. Прилежащие углы в плоских геометрических фигурах равны друг другу, поэтому ∠ODA = ∠OBC. Аналогично, ∠ODB = ∠OAC.

Так как векторы OA−→−, OB−→− и OC−→− даны в условии, нам нужно получить вектор OD−→−. Мы можем представить его как сумму векторов OA−→− и AD−→−, так как вектор OD−→− является результатом перемещения точки O на вектор AD−→−.

Используя теорему о векторной сумме, можем записать:

OD−→− = OA−→− + AD−→−.

Заметим, что вектор AD−→− можно выразить через вектор BC−→−, так как по условию задачи AD = 8BC.

Тогда получим:

OD−→− = OA−→− + 8BC−→−.

Теперь осталось выразить вектор BC−→− через векторы OA−→−, OB−→− и OC−→−.

Используем свойство векторов, согласно которому векторное произведение равно нулю, если векторы коллинеарны или противоположно направлены.

Поскольку BC−→− является диагональю трапеции ABCD и параллелен отрезку AD−→−, то BC−→− коллинеарен вектору AD−→−. Следовательно, векторное произведение BC−→− и AD−→− равно нулю.

Теперь представим, что вектор AD−→− является линейной комбинацией векторов OA−→−, OB−→− и OC−→−:

AD−→− = aOA−→− + bOB−→− + cOC−→−.

Требуется найти коэффициенты a, b и c. Для этого проделаем следующее:

aOA−→− + bOB−→− + cOC−→− = BC−→−.

Поскольку AD−→− и BC−→− имеют одинаковое направление и коллинеарны, то их координаты должны быть пропорциональны.

Тогда можно записать следующую систему уравнений:

a + b + c = 0,
a - b = 0,
a - c = 8.

Решая данную систему, найдем значения коэффициентов: a = 4, b = 4 и c = -4.

Теперь можем выразить вектор BC−→− через векторы OA−→−, OB−→− и OC−→−:

BC−→− = 4OA−→− + 4OB−→− - 4OC−→−.

Заменяем вектор BC−→− в предыдущем выражении для вектора OD−→−:

OD−→− = OA−→− + 8(4OA−→− + 4OB−→− - 4OC−→−).

Упрощаем:

OD−→− = OA−→− + 32OA−→− + 32OB−→− - 32OC−→−.

Таким образом, окончательный ответ:

OD−→− = 33OA−→− + 32OB−→− - 32OC−→−.