Дана матрица А, В,С и число q. Найти матрицу D=AB+qC.
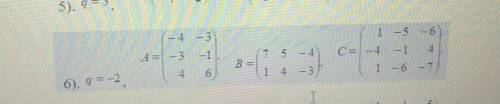
Другие вопросы по теме Математика
Популярные вопросы
- Догляд за комбінованою шкірою...
3 - Я слышал об отличной волонтерской программе. Что мы там будем делать?...
2 - Памагите очень сильно надо...
2 - конституция РФ охраняется ___а) в особом порядкеб) в упрощённом порядкев)...
3 - Давление в водопроводе равно 1,4•105 Па. Рассчитай,с какой силой...
1 - Про какую страну идет речь?? Средний доход на душу населения: 88,222...
3 - Синус х = - корень из 2/2 косинус х 1/2синус х = - корень из 3/2косинус...
1 - Прямые а || b. Найти ∠4, если ∠3 = 98’ а) 82 градуса б) 90 градусов...
3 - 6-тапсырма. Мәтіндегі қарамен берілген сөйлемд шаққа айналдырып жазыңдар....
2 - с заданием на времена, если можно то с объяснением...
2
Матрицами мы называем прямоугольные таблицы, состоящие из элементов (чисел), разделенных на строки и столбцы. В данном случае у нас есть матрицы А, В, С и число q.
Для начала, нам необходимо умножить матрицу А на матрицу В. Умножение матриц осуществляется путем совмещения элементов строк матрицы А с соответствующими элементами столбцов матрицы В, с последующим суммированием произведений этих элементов. Полученные суммы записываются в новую матрицу, называемую произведением матриц А и В.
Произведение матрицы А размера m × n на матрицу В размера n × p будет иметь размерность m × p.
Для выполнения умножения матрицы А на матрицу В, мы должны умножить каждый элемент строки А на соответствующий элемент столбца В, а затем сложить эти произведения.
Таким образом, получим матрицу P = AB.
Далее, нам нужно умножить матрицу С на число q. Это означает, что каждый элемент матрицы С надо умножить на q.
Полученное произведение, обозначенное как R = qC, будет иметь такую же размерность, как и матрица С.
В результате, чтобы получить матрицу D = AB + qC, мы должны сложить матрицы P и R.
То есть, для каждого элемента матрицы P и R, мы складываем соответствующие элементы и записываем в новую матрицу D.
Итак, общий алгоритм решения задачи будет выглядеть следующим образом:
1. Умножаем матрицу А размера 2×2 на матрицу B размера 2×2 по правилам умножения матриц. Получаем матрицу P.
P[1][1] = A[1][1] * B[1][1] + A[1][2] * B[2][1]
P[1][2] = A[1][1] * B[1][2] + A[1][2] * B[2][2]
P[2][1] = A[2][1] * B[1][1] + A[2][2] * B[2][1]
P[2][2] = A[2][1] * B[1][2] + A[2][2] * B[2][2]
2. Умножаем матрицу C размера 2×2 на число q.
R[1][1] = q * C[1][1]
R[1][2] = q * C[1][2]
R[2][1] = q * C[2][1]
R[2][2] = q * C[2][2]
3. Складываем матрицы P и R.
D[1][1] = P[1][1] + R[1][1]
D[1][2] = P[1][2] + R[1][2]
D[2][1] = P[2][1] + R[2][1]
D[2][2] = P[2][2] + R[2][2]
Таким образом, получим матрицу D = AB + qC, размерностью 2×2.
Надеюсь, это понятно и поможет вам в решении данной задачи!