1. Математика
  2. Дана функция z= xe^(-y/x)

Дана функция z= xe^(-y/x) . Показать, что... Задание смотреть на фото


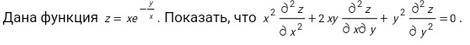
Дана функция z= xe^(-y/x) . Показать, что... Задание смотреть на фото

lubova1984 lubova1984    3   09.04.2021 19:37    1

Ответы
lenamarydina lenamarydina  09.05.2021 19:38

Пошаговое объяснение:

сначала найдем все нужные частные производные

\displaystyle \frac{\delta z}{\delta x} =\frac{ye^{-y/x}}{x^2} \qquad \frac{\delta^2 z}{\delta x^2} = \bigg (\frac{ye^{-y/x}}{x^2} \bigg )'_x=\frac{-2xye^{-y/x}+y^2e^{-y/x}}{x^4}

\displaystyle \frac{\delta z}{\delta y} =-\frac{e^{-y/x}}{x} \qquad \frac{\delta^2 z}{\delta y^2} =\bigg (-\frac{e^{-y/x}}{x}\bigg )'_y=\frac{e^{-y/x}}{x^2}

\displaystyle \frac{\delta^2 z}{\delta x \delta y} =\bigg (\frac{\delta z}{\delta x} \bigg )'_y=\bigg (\frac{ye^{-y/x}}{x^2} \bigg )'_y=\frac{xe^{-y/x}-ye^{-y/x}}{x^3}

ну вот. теперь эту е в степени -у/х я вынесу за скобки и, поскольку выражение  приравнивается к 0, вообще об оэтом е забуду

и получится вот что

\displaystyle x^2*\frac{-2xy+y^2}{x^4} +2xy*\frac{x-y}{x^3} +y^2*\frac{1}{x^2} =\frac{-2xy+y^2+2xy-2y^2+y^2}{x^2} =0

что и требовалось доказать.....

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
DozZzuM DozZzuM  16.09.2019 00:20
Диаметр окружности равен 4,08 см. значение числа π≈3,14. определи длину c этой окружности (с точностью до сотых)....
влад2314 влад2314  16.09.2019 00:20
Вупаковке 4 йогурта .сколько йогуртов в 4таких упаковках?...
Urinasonya Urinasonya  16.09.2019 00:20
Бабушка купила по одинаковой цене 15 саженцев уруюка и23 саженца яблони за всю покупку она заплатила 4560 сколько тенге заплатила. бабушка за саженцы урюка. за саженцы яблони. сфоткойте....
volkovaales0308 volkovaales0308  16.09.2019 00:20
Аравно 14дм в равно неизвестно в 2 раза меньше чем а а с неизвестно но на 3дм больше чем в...
catnizamova catnizamova  16.09.2019 00:20
Запишите в виде десятичных дробей числа 2 3/10,5 7/10,6 49/100,3 419/1000....
valeravolc1990o valeravolc1990o  16.09.2019 00:20
Нужно! первое: 1/4 его равны 80. второе: 1/10 его равны 10. третье: 1/2 его равны 30....
sataevaelsa sataevaelsa  16.09.2019 00:20
А) из 500 ответов, присланных на вопрос телевикторины, правильными оказались 150. найдите отношение числа правильных ответов. сколько процентов участников викторины ответило правильно?...
досметова досметова  16.09.2019 00:20
15 найдите значение выражения: 1)1290+х*у.если х=306. у=405 2)(t+l)*250, если t=499. l=201. с действиями...
Miratovich Miratovich  16.09.2019 00:20
12 рабочих асфальтировали улицу 21 день .сколько рабочих необходимо чтобы выполнить всю эту работу за 14 дней (если производительность труда и условия работы прежние)? надо пропорцией...
Forkier Forkier  16.09.2019 00:20
Не пользуясь таблицей простых чисел, докажите, что число: а) 29; б )41; в) 53; г) 59 является простым....

Популярные вопросы