1. Математика
  2. Дана функция распределения

Дана функция распределения f(x). Найти дисперсию D(x)

tima0204zhan tima0204zhan    3   05.03.2020 20:14    0

Ответы
myrrr14 myrrr14  11.10.2020 19:35

Здесь случайная величина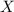 X - непрерывна.

Найдем плотность распределения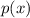 p(x), как производную от функции распределения F(x):

p(x)=F'(x)=\displaystyle \left \{ {{0,~~ x\leq 0,~~~ x2} \atop {\dfrac{x}{2},~~~~~~~ 0

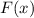Математическое ожидание непрерывной случайной величины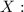 X:

MX=\displaystyle \int\limits^a_b {x\cdot p(x)} \, dx =\int\limits^2_0\dfrac{x^2}{2}dx=\dfrac{x^3}{6}\bigg|^2_0=\dfrac{2^3}{6}=\dfrac{4}{3}

Найдем теперь дисперсию

DX=\displaystyle MX^2-(MX)^2=\int\limits^a_b x^2p(x)dx-(MX)^2=\int\limits^2_0\dfrac{x^3}{2}dx-\left(\dfrac{4}{3}\right)^2=\\ \\ =\dfrac{x^4}{8}\bigg|^2_0-\dfrac{16}{9}=\dfrac{2^4}{8}-\dfrac{16}{9}=2-\dfrac{16}{9}=\dfrac{2}{9}

ответ: 2/9.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
SonyaKot1 SonyaKot1  22.04.2021 19:36
12. Денису надо было решить 20 задач, из них он уже решил 13 задач. Сколько процентов всех задач уже решил Денис?​...
SergeyPomoshnik SergeyPomoshnik  22.04.2021 19:36
Біля школи росло 8 берізок, кленів у 3 рази більше, ніж берізок, а ялин — наTменше, ніж берізок Кленів разом. Скіль-ки ялин росло біля школи? ?​...
StalinReal StalinReal  22.04.2021 19:37
Ширина прямокутного парам лепіпеда деревнює 3, 6 см, що становить 0,36 його довжини, а висота становить 0,42 довжини. обчисліть об єм паралелепіпеда...
привет888 привет888  22.04.2021 19:37
Решить примеры: а)-5,23⋅1,6= б)-6,27⋅(-0,13)= в)16,45:(-4,7)= г)1,702:(-3,7)=...
Balthazar1 Balthazar1  22.04.2021 19:37
при використанні в системі охолодження автомобіля вода утворюється накип і витрата пального може зрости на 10%.Якої витрати пального можно чекати після виделання накипу,...
wehhc wehhc  22.04.2021 19:38
Uери с 520 км. О8 годині ранио Відстань між містамиіз міст одночасно виїхали назустріч один одномуавтобуси й прибули на певну автостанцію о 12 гоні. З якою швидкістю...
ГКПС ГКПС  22.04.2021 19:38
Есть три комнаты, на двери каждой из них — табличка. А написано на табличках вот что: На первой: «В этой комнате — принцесса». На второй: «В этой комнате сидит дракон»....
vasiliybondaroxq3j4 vasiliybondaroxq3j4  22.04.2021 19:38
Постройте график прямой пропорциональности Y=-1/5x...
kill2021 kill2021  22.04.2021 19:39
1266. Диаметр окружности с центром в точке А равен 6 см (рис. 8.9). Расстояние меж-ду точками А и В равно 5 см. Точка Dобщая точка этих окружностей. Найдитедиаметр окружности...
mictermixa1 mictermixa1  02.07.2019 22:40
7*9*5+54*76=**718*: поставьте место звездочек цифры...

Популярные вопросы