Дана функция двух переменных . Проверить, выполняется ли тождество
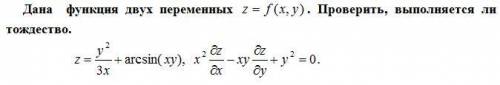
Другие вопросы по теме Математика
Популярные вопросы
- Сколько требуется угля для паровоза мощностью в 2,8 мвт, идущего...
1 - Можно с объяснением. при каком условии температура кипения воды...
3 - Описание персонажей в пьесы два окошка...
1 - Укажите варианты ответов, в которых в обоих словах одного ряда пропущена...
2 - На 2 фотографии номер 6 а 1 фотографию полностью...
3 - Всосуде ёмкостью 8л находится воздух при нормальном давлении и температуре...
3 - Какое слово скажет спрайт если ввести число 49...
3 - Какое соотношение не изменяется при изохорном процессе? а) 0v=const...
2 - Сізге саяхаттау өте ұнайды. ел-жер көру үшін кезекті саяхатыңызда...
1 - Отличия прудовика и беззубки...
3
подставляем в равенство:
равенство выполняется.