1. Математика
  2. Дана арифметическая прогрессия

Дана арифметическая прогрессия 2 6 10 найдите сумму первых шести членов

bryazgin98p06isp bryazgin98p06isp    2   02.09.2019 20:50    7

Ответы
mavlud111 mavlud111  06.10.2020 13:09

Член арифметической прогрессии (начиная со второго) задаётся формулой:

aₙ = a₁+(n-1)·d,  n = 2, 3, 4, ...

a₁ - первый член прогрессии, в данном случаи a₁=2.

d - разность ариф. прог. d =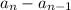 a_n-a_{n-1} = 6-2 = 4

Сумма первых n членов ариф. прог. вычисляется по формуле:

S_n=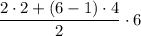\dfrac{a_1+a_n}{2} \cdot n=\dfrac{a_1+a_1+(n-1)\cdot d}{2}\cdot n=\\\\=\dfrac{2a_1+(n-1)\cdot d}{2} \cdot n

S₆ = \dfrac{2\cdot 2+(6-1)\cdot 4}{2} \cdot 6 = (4+5·4)·3 = 24·3 = 72

ответ: 72.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
BlackVaiNor BlackVaiNor  17.01.2021 23:47
Для перевозки груза автомобилю с грузоподъемностью 7,5 тонн пришлосьсделать 12 рейсов, Сколькорейсовпридется сделатьавтомобилюгрузоподъемностью 9 тонн для перевозки этого...
аза00 аза00  17.01.2021 23:48
Масштаб карти 1:2000000 відстань між двома містами на карті 2,6см знайди відстань місцевості(в кілометри) ​...
shaluni2005 shaluni2005  17.01.2021 23:51
При решении задач обязательный рисунок и запись «Дано». Комментировать решение коротко. № 1. Осевой сечение цилиндра квадрат, площадь которого 196 см2. Найти радиус основания...
kazimirova2009 kazimirova2009  17.01.2021 23:53
МАТЕМАТИЧ(ПРОДОВЖЕННЯ)7 год 45 + 1 год 15 хв) : 90 хв;​...
Thfhgdrhd Thfhgdrhd  17.01.2021 23:55
При розв язуваннi задач обов язковий рисунок та запис «Дано». Коментувати розв язок коротко. № 1. Осьовий перерiз цилiндра квадрат, площа якого 196 см2. Знайти радiус основи...
SpottedJay SpottedJay  17.01.2021 23:55
СОВСЕМ НИЧЕГО НЕ ПОНИМАЮ:(​...
ProstoSashaProsto ProstoSashaProsto  21.01.2021 21:31
Обувной отдел магазина за день продал 12 пар мужских ботинок, размеры которых равны 40; 44, 43, 45, 42, 43, 41, 44, 43, 43, 41; 45. Сгрупированный ряд этиX ДаННЫХ Имеет...
benblast benblast  21.01.2021 21:31
Тек бул 1 класстың есебі бұған менің даже басым жетпей отр​...
Map21 Map21  21.01.2021 21:31
Құрылымы күрделі теңдеулер. Бекіту Келесі теңдеу қандай болуға тиіс?Ойлан.х•3=15ו6=30х •12=60||​...
nikita06556 nikita06556  21.01.2021 21:31
В одной миле примерно 1609м.Автомобиль миль.найди пройденное автомобилем расстояние в километрах и метрах. (можно с условием)​...

Популярные вопросы