1. Математика
  2. Дан треугольник abc где а(1;

Дан треугольник abc где а(1; 2) b(0; 3) c(-2; -1). найти периметр его и угол а

дана403 дана403    2   06.10.2019 23:07    3

Ответы
tarringate tarringate  10.10.2020 00:33

Пошаговое объяснение:

AB=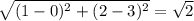\sqrt{(1-0)^{2}+(2-3)^{2} } =\sqrt{2}

AC=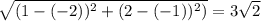\sqrt{(1-(-2))^{2}+(2-(-1))^{2})}=3\sqrt{2}

BC=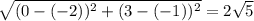\sqrt{(0-(-2))^{2}+(3-(-1))^{2}} = 2\sqrt{5}

Периметр равен сумме сторон:

Р =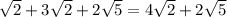\sqrt{2}+3\sqrt{2}+2\sqrt{5}=4\sqrt{2}+2\sqrt{5}

Поскольку квадрат суммы двух катетов равен квадрату гипотенузы,

(\sqrt{2})^{2} + (3\sqrt{2})^{2} = (2\sqrt{5})^{2}

2 + 18 = 20

то данный трегольник прямоугольный, и угол А равен 90°

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Крошка21155 Крошка21155  05.02.2022 22:28
Модуль числа -8,4 равен?.....
NikitaPetrov1234 NikitaPetrov1234  05.02.2022 22:29
1 и 2 л 3 и 4 и 5 л 6 ? 7 и 8 л...
ПудинговыйГраф ПудинговыйГраф  05.02.2022 22:29
Разложить на множители: a) 16x4– 2,25y2z2; б) (4a – b)2- а2....
lelekasahsa7 lelekasahsa7  05.02.2022 22:34
1. - 0,2 0,3 Жауабы: 1,вибирайте на угад пассаны это реално работает...
dshaa14 dshaa14  05.02.2022 22:34
Спростіть вираз (х+2)(хв квадраті-2х+4)-х(х-3(х+3)...
tonia8 tonia8  05.02.2022 22:35
Ширина прямоугольного параллелепипеда равна 22см а длина на 15 см больше ширины а высота в 2 раза меньше ширины найди объём этого параллелепипеда...
angelenok1840 angelenok1840  05.02.2022 22:41
Решите уравнение |5x+6|=10 ,...
Nika5647 Nika5647  05.02.2022 22:45
(-14х+0,55):0,5=2/3х-170,9...
bulycheva0303 bulycheva0303  05.02.2022 22:45
За сор дам корону и 25 звёзд жду :)...
11martandreyp0bwg2 11martandreyp0bwg2  05.02.2022 22:45
Приведи sin157° к значению тригонометрической функции наименьшего положительного аргумента. ответ:-sin23 sin22cos67-cos67sin67...

Популярные вопросы