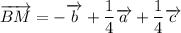Дан тетраэдр dabc, k-середина ребра ac, m-середина отрезка kd, вектор da=вектору a, вектор db=вектору b, вектор dc=вектору c. разложите вектор bm по векторам a,b,c.
Другие вопросы по теме Математика
Популярные вопросы
- Стереометрия В правильной четырехугольной пирамиде основная сторона...
3 - пытаюсь зарендерить видео в after effects cc 2015 выдаёт ошибку и...
3 - Задана система x^2+y^2=49 y=x^2+a 1)При якому найменшому додатному...
3 - Төл сөздерді, төлеу сөзге айналдырыңызші тез істеңіз дерші 15мин ең...
2 - Complete the zero and first conditional sentences with the correct...
2 - Конкурентні переваги України на світових ринках сільськогосподарської...
3 - Кто лучше ревенант или октейн? ...
1 - Розташуй в порядку збільшення виробництва електричного струму за регіонами...
2 - Сторона основания правильной шестиугольной пирамиды равна 6 см. Боковые...
3 - Как подписать фото в стиле 19 века?...
1
Достроим до параллелограмма ADCE, так как K - середина АС, то по правилу параллелограмма
Так как M - середина DK, то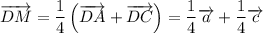
По правилу треугольника (из треугольника DMB)
ответ: