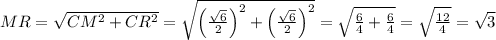Дан параллелепипед `abcda1b1c1d1`, где `ad=sqrt(3)/sqrt(2`; `dc=a(a1)=sqrt(6)`. найдите расстояние от точки, находящейся на середине dc до прямой br, где- r середина cc1
Другие вопросы по теме Математика
Популярные вопросы
- Выбери• • Sjjrkrkrjjrkd• •S...
3 - В каком предложении есть вводное слово (знаки препинания не расставлены!)?...
2 - Записать текст, поставить ударение в словах, выделить корень,...
2 - Решите кому не трудно : -4*(19а+1)-15=-19...
3 - Упражнения по теме Слова категории состояния Упражнение 1. Найдите...
2 - На какие классы по своему назначению подразделяются электронагревательные...
2 - Выбери слово, запиши и переведи предложение.1. Would you like...
3 - Пиріжків із капустою купили на 3 більше, ніж пиріжків з яблуками.Скільки...
2 - ПРЕКРАСНЫЕ ХИМИКИ Допишите нужное слово: 1) Сложные вещества,...
1 - РЕШИТЬ О=9 560 · 590 Л=35 200 · 708 Ф=67 409 · 4 070 И=8403 ·...
2
Пусть М - точка, находящаяся на середине DC.
Расстояние от М то BR - это длина перпендикуляра, опущенного из M на BR, т.е. длина отрезка MR (MR⊥BR, т.к. плоскости, в которых они лежат, перпендикулярны).
т.к. M и R - середины сторон DC и CC₁ соответственно.
Таким образом, из ΔMRC по т.Пифагора