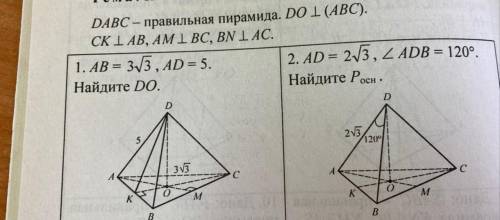
DABC- правильная пирамида DO перпендикулярен (ABC)
CK перпендикулярен AB
AM перпендикулярен BC
BN перпендикулярен AC

1. AB = 3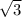
AD = 5
Найдите DO

2. AD = 2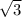
Угол ADB = 120
Найдите Росн.

Добрый день! Давайте решим задачу поочередно.

1. Нам дано, что DABC - правильная пирамида, DO перпендикулярен (ABC), CK перпендикулярен AB, AM перпендикулярен BC, BN перпендикулярен AC. Известно, что AB = 3√3 и AD = 5. Нужно найти DO.

Для решения задачи воспользуемся теоремой Пифагора. Используя треугольник ABD, можем записать:

AB² = AD² + BD².

Заметим, что BD это DO, так как BD и DO - это одна и та же линия. Таким образом, получаем:

(3√3)² = 5² + DO².

9 * 3 = 25 + DO².

27 = 25 + DO².

DO² = 27 - 25.

DO² = 2.

DO = √2.

Ответ: DO = √2.

2. Во второй задаче нам дано, что AD = 2√3 и угол ADB = 120°. Нужно найти Росн.

Росн - это угол между плоскостью ABCD и плоскостью BCD.

Мы знаем, что сумма углов BDA и CDB равна 180°, так как они составляют прямой угол в плоскости BCD. Угол BDA равен 120°, поэтому угол CDB равен 180° - 120° = 60°.

Так как угол BCD является внешним углом треугольника BDA, то он равен сумме углов BDA и CDB, то есть 120° + 60° = 180°.

Значит, Росн = 180°.

Ответ: Росн = 180°.