Д/У.
РЕШИТЬ ХОТЯ-БЫ 2 ПРИМЕРА.
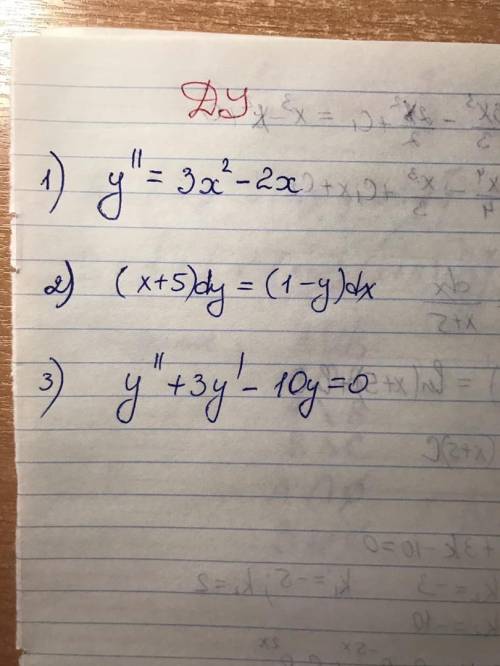
Другие вопросы по теме Математика
Популярные вопросы
- Корень из169-5корень из18 *корень из8...
2 - Заповедники национальные парки россии(название где находится когда...
3 - .(Спильнокореневе слово до -мисто, зброя)....
3 - .(Одна сторона триугольника равна 10 см она на 2см меньше второй...
3 - Велосипедист проїхав 67 км. 3 год він їхав до обіду і 2 год після...
2 - .(2боровика,2 подберезовика и 2 подосиновика. расположи их в 3...
1 - Из вершины прямого углапроведен луч так, что он делит прямой угол...
2 - Решите уравнение: 1,2-(2х-(х--0,8)=-2х...
2 - .(Вмагазин 40 ящиков апельсинов по 15 кг. в каждом и продали их...
2 - Y=(x-1)( в квадрате)+2 как её описать!...
1
ответ: 1) y=1/4*x⁴-1/3*x³+C1*x+C2, где С1 и С2 - произвольные постоянные.
2) y=(x+5+C)/(x+5), где С≠0.
3) y=C1*e^(2*x)+C2*e^(-5*x), где С1 и С2 - произвольные постоянные.
Пошаговое объяснение:
1) y'=∫(3*x²-2*x)*dx=3*∫x²*dx-2*∫x*dx=x³-x²+C1; y=∫y'*dx=∫x³*dx-∫x²*dx+C1*∫dx=1/4*x⁴-1/3*x³+C1*x+C2, где С1 и С2 - произвольные постоянные.
2) Разделив уравнение на произведение (x+5)*(1-y), получаем уравнение dy/(1-y)=dx/(x+5), или dy/(y-1)+dx/(x+5)=0, или d(y-1)/(y-1)+d(x+5)/(x+5)=0. Интегрируя, находим ln/y-1/+ln/x+5/=ln/C/, или (y-1)*(x+5)=C, где C - произвольная, но не равная нулю, постоянная. Отсюда y-1=C/(x+5) и y=(x+5+C)/(x+5).
3) Перед нами - однородное ЛДУ 2 порядка с постоянными коэффициентами. Для его решения составляем характеристическое уравнение: k²+3*k-10=0. Оно имеет действительные и притом различные корни k1=2 и k2=-5, поэтому y=C1*e^(2*x)+C2*e^(-5*x), где С1 и С2 - произвольные постоянные.