Діагональ основи правильної чотирикутної призми дорівнює 2√2 см, а діагональ призми дорівнює 3 см. Знайдіть площу повної поверхні призми. Можно просто малюнок. Дякую.

1) По теореме Пифагора  найдём сторону квадрата в основании.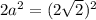

см

2) Диагональ основания, диагональ призмы и высота призмы образуют прямоугольный треугольник, в котором

2√2 см - катет;

3 см - диагональ

h - катет (она же  высота призмы)

По теореме Пифагора  найдём h.

см

3)

  см²

  см²

  см²

  см²

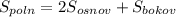
ответ:  16 см²