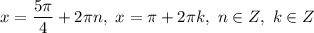|cosx-2sinx|+cosx=0
Может ли кто объяснить решение этого уравнения?
У меня получаеться +-3pi/4 +2pik и pi +2pik
ответ: 3pi/4 + 2pik, pi+2pik (не могу понять почему не +-3pi/4)
Другие вопросы по теме Математика
Популярные вопросы
- Подскажите, как написать структурную формулу натрия? ?...
1 - 1.в какой части материка больше всего водоёмов.почему? 2.что означает...
3 - Назовите события, которые произошли в период смуты. расположите...
2 - 7х^2-3х=0 решить квадратное уравнение...
2 - Первое число 47,второе число23,а третье число меньше суммы двух...
3 - Во вторник собрали 24 т. лука, а в среду 260 ц. весь лук расфосовали...
3 - На арене цирка 2 жонглёра, а акробатов - на 5 больше. сколько всего...
3 - Сочинить сказку о чем шепчутся раки...
2 - Врешение . составить уравнение и решить . расстояние между поселками...
3 - 99 . сочинение-репортаж по картине сайкиной детская спортивная...
2
1) Решим неравенство:
2) Решим первое уравнение совокупности:
Здесь, если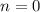 , то
, то 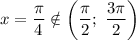 , а если
, а если 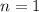 , то
, то 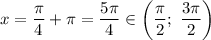
Таким образом, наименьший положительный период должен быть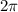 , поэтому
, поэтому
3) Решим второе уравнение совокупности:
Здесь, если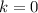 , то
, то ![x = 0 \notin \left[\dfrac{\pi}{2}; \ \dfrac{3\pi}{2} \right]](/tpl/images/1067/3233/9590b.png) , а если
, а если 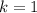 , то
, то ![x = \pi \in \left[\dfrac{\pi}{2}; \ \dfrac{3\pi}{2} \right]](/tpl/images/1067/3233/9c25f.png)
Таким образом, наименьший положительный период должен быть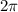 , поэтому
, поэтому
ответ: