Cos⁴x=cos2x
Решите через приведение к биквадратному, если всё таки решаете через формулу cos²x=(1+cos2x)/2, не сводя уравнение к биквадратному , то распишите решение как можно подробнее.
Другие вопросы по теме Математика
Популярные вопросы
- Чого навчає мене захар беркут прикладом свого життя написать...
1 - Переведите на : 1) я встречу друга завтра. 2) анна будет знаменитой...
3 - Раскройте скобки: (3m-4n)+(5m+3n)+n-7m...
2 - За 3 дні автомобіль проїхав a км.прешого дня він проїхав 300,а...
3 - Решите уравнение: 1.1)6x-1.3=-2x+2.2 2).8x-5.6=6.6x-8.4 2. методом...
2 - Зяких атомів складається кухонна сіль...
1 - Вкаком городе древнего мира на центральной площади стоял камень,...
3 - Родственные слова-река.печь.свеча.ветка.яблоко...
3 - Определить связи слов в словосочетаниях браться за работу, стремление...
3 - Вот в языке к примеру this is a camera this это типо это слова...
3
cos⁴x=2cos²-1 (раскрыли по формуле косинуса двойного угла)
Пусть cos²x=a, a ∈ [-1; 1]
a²-2a+1=0
D = 4 - 4 = 0 ⇒ a = -b/2a (это формула единственного корня, когда D равен нулю)
a = 2 : 2 = 1
Обратная замена: cos²x = 1
cosx = +-1
x=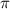 + 2
+ 2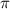 n. n∈z и x= 2
n. n∈z и x= 2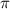 n, n∈z (теперь объединим и получим ответ)
n, n∈z (теперь объединим и получим ответ)
ответ: x =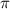 n , n ∈ z
n , n ∈ z