Cos a = 8\17, 3п\2< а < 2п найти sin 2a распишите решение
Ответы
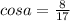 ,
, 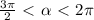
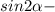 ?
?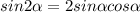
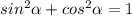
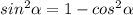
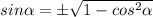
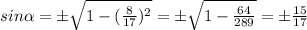 так как
так как 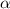 ∈
∈ 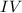 четверти, то
четверти, то 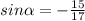
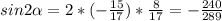
Другие вопросы по теме Математика
Популярные вопросы
- Қорық туралы мақала жазыңдар. керек...
1 - СЕН ЗЕРТТЕУШІСІҢ Әрбір сандар тізбегінің заңдылығын анықтап, қалдырыл-ған...
1 - Структурні компоненти статевої культури суспільства?...
1 - С Составьте и запишите предложения по схемаТ 5451)11, но22)потому чт199...
1 - Составьте текст интервью с Варварой Суворовой. Какие вопросы вы задали бы...
1 - Кейінгі үздік құбылыс» деп баға берген? Пікіріңде күшейткіш демеулік шылаулар...
1 - 3 Талдау 1. Мысалда келтірілген жалғыз Бидай туралы өз ойларынды білдірін-дер,...
1 - 4 тапсырма повесть оқып шығып тақрыбы мен идеясын анықтаңдар Бөлімдерге ат...
3 - Как делить с проверкой и с остатком 50:24=...
3 - Сравните полученную из стихотворения информацию с данным кластером. Сделайте...
1