Cледом квадратной матрицы называется сумма элементов её главной диагонали. Доказать, что для любых матриц A и B таких, что имеют
смысл оба произведения AB и BA, следы матриц AB и BA совпадают
Другие вопросы по теме Математика
Популярные вопросы
- При каких значениях х верно равенство: 2 : х = 0,1 20 200 2 0,2 РЕБЯТА...
1 - 3 класс вычисли с объяснением выполни проверку...
2 - 42. Прочитайте фразы и объясните, почему употреблены или не употреблены...
2 - Перед вами опорные схемы, иллюстрирующие, чем можно заменить зна-...
1 - Доброе утро! за выходные написать сочинение по рассказу Муму Примерный...
2 - Connect the writer and his work: a) Ivan Turgenev 1. Crime and Punishment...
1 - взаимоотношение казахов со среднеазиатскими ханствами Доброй день...
1 - Решите уравнение12 – 4(х – 3) – 2x = (5 – 3x) + 9...
1 - Задание #1 Вопрос: Определите в приведённом ниже перечне изменений...
2 - Хто був рушійною силою в національно-визвольній війні наймані кримськівсі...
3
Пусть даны матрицы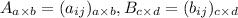 . Т.к. определено произведение
. Т.к. определено произведение 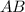 ,
, 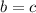 . Т.к. определено произведение
. Т.к. определено произведение 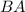 ,
, 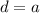 .
.
А значит даны матрицы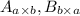
Пусть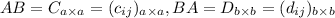 .
.
По определению,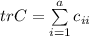 .
. 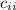 - сумма произведений соответствующих элементов iой строки матрицы A и iого столбца матрицы B, т.е.
- сумма произведений соответствующих элементов iой строки матрицы A и iого столбца матрицы B, т.е. 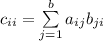 =>
=> 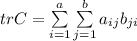
Аналогично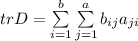
Т.к. пределы суммирования не зависят от переменных, то знаки суммирования можно поменять местами: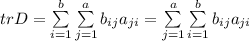
А теперь заметим, что, переобозначив переменные![[i\to j;j\to i]](/tpl/images/3824/0204/a62a7.png) , получим
, получим 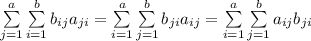 - а это и означает, что
- а это и означает, что 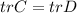
Ч.т.д.