Числа n+1 и 2n+1 являются точными квадратами .докажите, что n кратно 24

Т.к.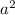 нечетно, то и нечетно, а значит и 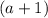четные. Пусть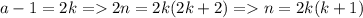

Из двух последовательных натуральных чисел одно кратно 2. Значит n кратно 4.

Четность и 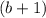одинакова. А значит они оба четные. Пусть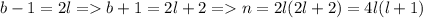

Из двух последовательных натуральных чисел одно кратно 2. Значит n кратно 8.

l дает остаток 1 при делении на 3. Тогда n дает остаток 2 при делении на 3. Тогда 2n+1 дает остаток 2 при делении на 3. Но 2n+1 - точный квадрат, а точные квадраты либо кратны 3, либо дают остаток 1 при делении на 3. Противоречиеl дает остаток 2 при делении на 3. Тогда n дает остаток 0 при делении на 3.l дает остаток 0 при делении на 3. Тогда n дает остаток 0 при делении на 3.

А значит n кратно 3.

Тогда n кратно 3*8=24