чи може вершина параболи f(x)=x²-2(a+1)x+(2018/a) лежати в 1 чверті при деякому значенні параметра a?

Question

Математика: чи може вершина параболи f(x)=x²-2(a+1)x+(2018/a) лежати в 1 чверті при деякому значенні параметра a? Відповідь обґрунтуйте

Zefirka08 · Answer

Положение вершины параболы определяется по формуле:

хо = -в/2а.

Подставим коэффициенты из заданного уравнения.

хо = -(-2(а+1))/2*1 = а + 1.

Отсюда параметр а = хо - 1.

Чтобы вершина была правее оси Оу, значение хо должно быть положительным. То есть хо = а + 1 > 0.

Отсюда a > -1.

Далее, чтобы вершина была выше оси Ох, значение у должно быть больше 0: x²-2(a+1)x+(2018/a) > 0.

D = 4(a+1)² - 4*1*(2018/a) = 4a² + 8a + 4 - (4072/a).

Чтобы вершина была выше оси Ох надо, чтобы дискриминант был меньше 0: 4a² + 8a + 4 - (4072/a) < 0.

Получаем выражение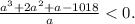 $\frac{a^3+2a^2+a-1018}{a}$

Из него получаем a < 9,4043.

С учётом, что а не равно 0, получаем ответ.

ответ: -1 < a < 0, 0 < a < 9,4043.

чи може вершина параболи f(x)=x²-2(a+1)x+(2018/a) лежати в 1 чверті при деякому значенні параметра a? Відповідь обґрунтуйте