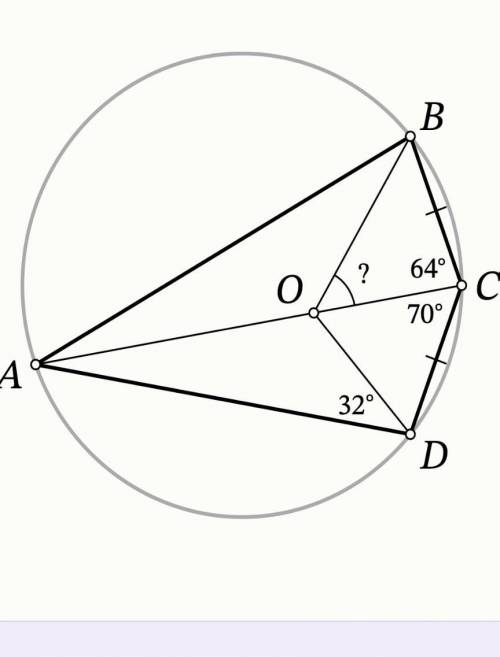
Четырехугольник ABCD вписан в окружность. Известно, что BC=CD, ∠BCA=64,  ∠ACD=70∘.  На отрезке AC отмечена точка O такая, что ∠ADO=32∘. Сколько градусов составляет угол BOC?

Для решения данной задачи мы можем использовать следующие свойства вписанных четырехугольников:

1. Вписанные углы в одну дугу равны между собой.
2. Биссектриса угла вписанного четырехугольника является перпендикуляром к его диагоналям.

Давайте рассмотрим каждый шаг подробно:

1. Поскольку ABCD - вписанный четырехугольник, мы знаем, что углы BCD и BAD равны между собой.
∠BCD = ∠BAD (свойство вписанных углов)

2. Также по условию задачи, BC = CD. Это означает, что треугольник BCD равнобедренный.
Из равнобедренности треугольника BCD следует, что ∠BCD = ∠CDB.

3. Вспомним, что BO является биссектрисой угла BCD.
Так как ∠BCD = ∠CDB, то ∠BCO = ∠CDO (свойство биссектрисы угла в равнобедренном треугольнике).

4. Введем новую точку E, которая является пересечением отрезков AO и BD.
Так как ∠ADO = 32°, то угол ODE также равен 32° (по свойству биссектрисы угла ADO).

5. Из равенства ∠BCO = ∠CDO следует, что угол BCO равен углу CDO.
Также можно заметить, что вписанный угол BCD имеет меру (70° + 70°) = 140°,
поскольку ∠ACD = 70° и ∠CDB = 70°.

6. Сумма углов треугольника CDO равна 180° (все углы треугольника в сумме дают 180°).
Мы уже знаем, что угол ODE = 32°, а угол CDO = 140°.
Таким образом, ∠COD = 180° - 32° - 140° = 8°.

7. Но мы хотим найти угол BOC, а не COD. Заметим, что угол BOC является вписанным углом,
и его мера равна половине меры смежного вписанного угла ∠BCD.
Таким образом, ∠BOC = 0,5 * ∠BCD = 0,5 * 140° = 70°.

Итак, угол BOC составляет 70°.