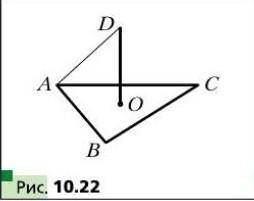
через центр O правильного треугольника ABC проведена прямая DO, перпендикулярная плоскости ABC (рис. 10.22). Найдите отрезок DO, если AB=6 см, DA=4 см
Другие вопросы по теме Математика
Популярные вопросы
- Один килограмм металлолома заменяет 2 1/2 кг богатой железом руды. сколько...
1 - Запишите в виде равенства тремя разными в 3 раза больше d...
1 - Тело, двигаясь равноускоренно, проходит последовательно два одинаковых отрезка...
1 - Есть ли однородные члены в предложении синими и зелеными искрами блестит...
2 - Какие крепости были построены при борисе годунове...
1 - Решить! систему неравеств { 3x+9 0 2x^2+5x+2≥0...
2 - Дайте краткий и понятный реферат на металл титан, то бишь возникновения,...
3 - Склади невеличку розповідь на тему день народження...
1 - Нарисуй линию горизонта для человека стоящего на ровной поверхности земли...
1 - Выражение: а(в 4 степени) * (9а(в квадрате) - 6а +1) и всё это выражение...
2
Дано: AB=6 см, DA=4 см
Первым шагом, давайте обратимся к свойству равнобедренного треугольника. В равнобедренном треугольнике, биссектриса угла основания проходит через центр окружности, описанной около этого треугольника. Так как ABC - правильный треугольник, плоскость треугольника является плоскостью симметрии и, следовательно, биссектриса угла ABD (то есть DO) проходит через центр O.
Далее, мы можем заметить, что DO является высотой треугольника ABD (потому что перпендикуляр от центра прямоугольного треугольника к его гипотенузе является высотой треугольника).
Поэтому, чтобы найти отрезок DO, нам нужно найти точку пересечения прямой AO (высоты треугольника ABD) и прямой BD (гипотенузы треугольника ABD). Для этого мы должны сначала найти длины отрезков AO и BD.
Воспользуемся теоремой Пифагора для треугольника ABD:
BD^2 = AB^2 - AD^2
BD^2 = 6^2 - 4^2
BD^2 = 36 - 16
BD^2 = 20
BD = √20
BD = 2√5 см
Далее, воспользуемся фактом, что в прямоугольном треугольнике, высота к гипотенузе является средним геометрическим между двумя сегментами гипотенузы.
DO = AO = BD/2
DO = 2√5/2
DO = √5 см
Ответ: Отрезок DO имеет длину √5 см.