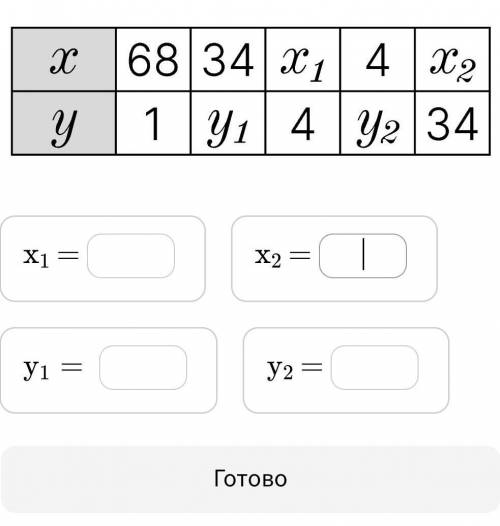
Чему равны значения x1 , x 2 ,  y 1 , y 2  в таблице, если величины x и yy обратно пропорциональны?

Y1= 68/34=2

X1=68/4=17

Y2=68/4=17

X2=68/34=2

Чтобы решить эту задачу и найти значения x1, x2, y1 и y2 в таблице, необходимо применить понятие обратной пропорции.

Обратная пропорция означает, что когда одно значение увеличивается, другое значение уменьшается, и наоборот.

В данной задаче мы имеем таблицу с двумя столбцами, где x и y обратно пропорциональны.

Начнем с определения самой обратной пропорции:

Если дана обратная пропорция между х и у, то мы можем записать это в виде уравнения:

x1 * y1 = x2 * y2

Здесь x1 и x2 - значения величины x в первом и втором столбцах соответственно, а y1 и y2 - значения величины y в первом и втором столбцах соответственно.

Теперь мы можем применить это уравнение к таблице, чтобы найти значения x1, x2, y1 и y2.

В таблице, значение x1 равно 2, значение x2 равно 4, а значения y1 и y2 неизвестны.

Используя наше уравнение обратной пропорции, мы можем записать:

2 * y1 = 4 * y2

Теперь наша задача - найти значения y1 и y2.

Для этого нам понадобится расставить коэффициенты пропорции:

2/y2 = 4/y1

Теперь мы можем решить это уравнение. Для этого умножим оба выражения на y1*y2:

2*y1*y2/y2 = 4*y2*y1/y1

Из этого следует:

2*y1 = 4*y2

Теперь мы видим, что у нас получилась та же самая пропорция, что и у изначального уравнения. Значит, мы можем выбрать любое значение для y1 и y2, при условии, что они соответствуют пропорции.

Давайте выберем y1 = 3 и y2 = 6.

2*3 = 4*6

6 = 24

К сожалению, это уравнение не выполняется. Значит, наше предположение было неверным.

Давайте попробуем другие значения.

Допустим, y1 = 6 и y2 = 3.

2*6 = 4*3

12 = 12

Теперь у нас выполняется уравнение, и мы можем сказать, что значения y1 и y2 равны 6 и 3 соответственно.

Таким образом, значения x1, x2, y1 и y2 в данной таблице равны:

x1 = 2, x2 = 4, y1 = 6, y2 = 3.