Боковое ребро двадцатиугольной правильной пирамиды равно 9, а высота пирамиды - 6. найдите радиус описанной около пирамиды сферы.

Рассмотрим шаровой сегмент, который образует пирамида.

h = 6.

r =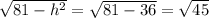

По теореме Пифагора:

1) Сложно представить двадцатиугольную правильную пирамиду, в основании которой правильный двадцатиугольник , но выглядит она примерно таким образом ( см. рисунок ):

точка О - центр сферы, которая лежит на высоте пирамиды

точка О1 - центр правильного двадцатиугольника

2) Рассмотрим ∆ SO1D:

По теореме Пифагора:

О1D² = 9² - 6² = 81 - 36 = 45

O1D = 3√5

AD = 2 × O1D = 2 × 3√5 = 6√5

3) Радиус описанной сферы равен радиусу окружности, описанной около треугольника SAD

S sad = 1/2 × SO1 × AD = 1/2 × 6 × 6√5 = 18√5

R = abc / 4S = ( 6√5 × 9 × 9 ) / ( 4 × 18√5 ) = 27 / 4 = 6_3/4 = 6, 75

ОТВЕТ: 6,75