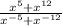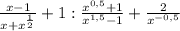
Боковая поверхность правильной четырехугольной призмы равна 48 см^2, а полная поверхность - 56 см^2. Найдите высоту призмы. 1) $\frac{x^{5}+x^{12} }{x^{-5}+x^{-12} }$ 2) $\frac{x-1}{x+x^{\frac{1}{2} } }+1 : \frac{x^{0,5}+1 }{x^{1,5} -1} +\frac{2}{x^{-0,5} }$

Ответы

Vitaminka123456789 06.09.2020 23:20

h=6 см

1) -1

Пошаговое объяснение:

Sбок.=48 см2

Sполн.=56 см2

Из формулы Sполн.=Sосн.+Sбок.

находим:

Sосн.=Sполн.-Sбок.=56-48=8 (см^2)

Так как основания правильной 4-х

угольной призмы - 2 квадрата

Sосн.=2а^2, отсюда

а=√Sосн.:2=√8:2=2 (см^2)

Зная сторону основания и Sбок.,

из формулы Sбок.=4аh найдем высоту h -

h=Sбок. : 4а=48:(4*2)=48:8=6 (см)

1) х^5+х^12/х^-5+х^-12=х^17/х^-17=-1

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

ggghh99 27.04.2021 11:42

vasiaska234 27.04.2021 11:43

barashinaa88 27.04.2021 11:44

SonicAndDash 27.04.2021 11:44

evzrezovatatya 27.04.2021 11:44

(1125+875)×18+4328 по действиям...

vmartynova77 27.04.2021 11:44

7(x - 2) + 2 = 2(x +3) + 7...

AlexxxM1 27.04.2021 11:44

Leonardo81 27.04.2021 11:44

6469678 27.04.2021 11:45

huh106 27.04.2021 11:46

Иврпз 2 кат ой нет ой да не не быстра фигу на...

Боковая поверхность правильной четырехугольной призмы равна 48 см^2, а полная поверхность - 56 см^2. Найдите высоту призмы. 1) 2)