1. Математика
  2. , без калькулятора и всë по

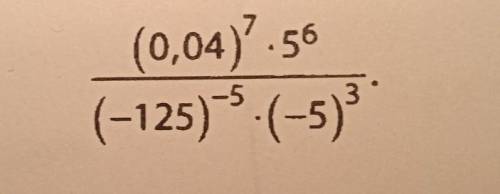
, без калькулятора и всë по действиям :)​


, без калькулятора и всë по действиям :)​

v0632039813 v0632039813    1   05.06.2021 23:23    0

Ответы
Игнор1 Игнор1  05.06.2021 23:30

\displaystyle \frac{(0.04)^7*5^6}{(-125)^{-5}*(-5)^3} \\ 1) ~~ \frac{(0.04)^7*\boldsymbol{5^3}}{(125)^{-5}} \\ \\ \\2) ~~ \frac{(0.04)^7*5^3}{(\frac{1}{125} )^\boldsymbol{5}}

\displaystyle 3) 125^5 * (0.04)^7*5^3 \\ \boldsymbol{(125*0.04=5)} 5^5*(0.04)^2*5^3 boldsymbol{0.04*5^2=0.2*5=1}5^8*(0.04)^2=5^4 = 625

ответ: 625

ПОКАЗАТЬ ОТВЕТЫ
habman habman  05.06.2021 23:30

625

Пошаговое объяснение:

 Выразим все множители в числителе дроби виде степеней с основанием 5

0.04=\frac{1}{25}=25^{-1} =(5^2)^{-1}=5^{-2}

Выразим все множители в знаменателе дроби виде степеней с основанием -5

-125=(-5)^3

 Тогда исходное выражение перепишется в виде

\frac{(0.04)^7\cdot5^6}{(-125)^{-5}\cdot (-5)^3}=\frac{(5^{-2})^7\cdot5^6}{((-5)^3)^{-5}\cdot (-5)^3}

 Пользуясь свойством степени, приведем все множители к стандартному виду

(5^{-2})^7=5^{-2\cdot7}=5^{-14}((-5)^3)^{-5}=(-5)^{3\cdot(-5)}=(-5)^{-15}

 Тогда

\frac{(5^{-2})^7\cdot5^6}{((-5)^3)^{-5}\cdot (-5)^3}=\frac{5^{-14}\cdot5^6}{(-5)^{-15}\cdot (-5)^3}

 Пользуясь свойством степени, произведем умножение отдельно в числителе и знаменателе

5^{-14}\cdot5^6=5^{-14+6}=5^{-8}(-5)^{-15}\cdot(-5)^3=(-5)^{-15+3}=(-5)^{-12}

 Также, т.к. в знаменателе дроби степень имеет отрицательное основание и чётную степень, то

(-5)^{-12}=5^{-12}

 Тогда

\frac{5^{-14}\cdot5^6}{(-5)^{-15}\cdot (-5)^3}=\frac{5^{-8}}{(-5)^{-12}}= \frac{5^{-8}}{5^{-12}}

 Пользуясь свойством степени, выполним деление

\frac{5^{-8}}{5^{-12}}=5^{-8-(-12)}=5^{-8+12}=5^4

 Окончательно

5^4=625

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
kadieva1976 kadieva1976  27.09.2019 06:10
На руси верили, что 11 ноября медведь ложится в берлогу и начинает сосать лапу. в период с 11 по 22 ноября медведь семь дней сосал переднюю лапу и пять дней — заднюю. также он...
аннасерб аннасерб  27.09.2019 06:10
От варки до магазина 168 метров а от магазина до дома в 3 раза меньше. сколько всего метров гена и чебурашка.когда вазвращались из парка домой заходя в магазин....
AHgpyxa AHgpyxa  27.09.2019 06:10
Найдите решение выражения 20,3-3•a. при a= 5,8...
06062007ивант 06062007ивант  27.09.2019 06:10
48а : 12, (11а*2) *0.1 и так далее. плз....
azerzhanovaa azerzhanovaa  27.09.2019 06:10
Решите , составив уравнение: доктор айболит взвешивает на своих весах воробьев и ласточек . 5 воребьев окозались тяжелее 6 ласточек. когда доктор айболит поменял местами одного...
altynbekova2003 altynbekova2003  27.09.2019 06:10
Вася купил 5 карандашей по 23 руб. и 2 альбома для рисования по 110 руб. сколько денег заплатила вася за всю покупку?...
lenamakar67 lenamakar67  27.09.2019 06:10
Из точки p к окружности с центром в точке о проведены касательные pa и pb(a и b точки касания). угол apb=90°. расстояние между точками касания ав равно √5. чему равно растояние...
Demonis666 Demonis666  27.09.2019 06:10
Когда крокодил гена жил в зоопарке в будний день к нему приходили 42 ребенка, а в повыходным- в 3 раза больше. сколько пришли к гене в пятницу и в субботу...
dianka0202 dianka0202  27.09.2019 06:10
Решить: (1400+1393,06+х)/3=1169,355 чему равен х?...
evgeniiantonov evgeniiantonov  27.09.2019 06:10
Одна целая семь восьмых делить на восемь целых одну третью равно икс делить на четыри девятых решить уравнение...

Популярные вопросы