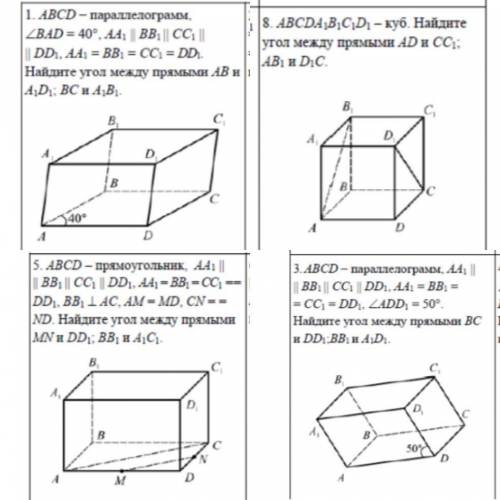
АВCD - прямоугольник, АA1 |I BB1 || CC1 ||DD1 , AA1=BB1=CC1=DD1, BB1 перпендикулярна AC, AM=MD,CN=ND.Hайдите угол между прямыми MN и DD1;BB1 и A1C1
Другие вопросы по теме Математика
Популярные вопросы
- 1.прочитайте.выпишите выделенные слова(это те которые большими буквами)подчеркните...
2 - Образуйте степени сравнения прилагательных: tom is.. than kate a)tall b)taller c)the...
3 - Какое слово лишнее: берег,огород,обед, играем...
3 - Как культура и религия взаимодействуют друг с другом...
1 - Как надо поступить,чтобы сильней остудить горячий чай : сразу бросить в него сахар...
3 - Глагол летит относится к 1 спряжению, почему окончание ит?...
3 - Сравни значения величин 70см-7дм, 4м-51дм, 95см-1м,6дм1см-60см....
3 - Сочинение в публицистическом стиле что важнее как жить или для чего жить...
1 - За круглый стол на 17 стульев в случайном порядке рассаживаются 15 мальчиков и 2...
2 - Какое слово лишнее: желток, железо, жёлтый...
2
1) Угол между прямыми MN и DD1:
У нас дан прямоугольник ABCD, где AB || CD и AD || BC. По условию, BB1 перпендикулярна AC.
Заметим, что прямая MN параллельна продолжению прямой AB за точку B и параллельна продолжению прямой CD за точку D.
Так как AB || CD и AC - это диагональ прямоугольника ABCD, то угол между прямыми MN и DD1 будет равен углу CDD1.
Также, известно, что AM = MD, то есть точка M делит отрезок CD пополам. То же самое верно и для точки N и отрезка AB.
Поэтому, угол CDD1 также делит отрезок DD1 пополам.
Таким образом, угол CDD1 является прямым углом, так как DD1 - это биссектриса угла CDD1.
2) Угол между прямыми BB1 и A1C1:
Для решения этой части задачи мы будем использовать свойства параллельных прямых.
Мы знаем, что BB1 и AC параллельны, поэтому угол между ними будет равен углу, образованному прямыми, пересекаемыми прямой C1A1.
Так как AB || CD и AA1 || BB1, то угол между прямыми BB1 и A1C1 будет равен углу C1AA1.
Также, заметим, что A1M = AM = MD, как мы уже установили.
Получаем, что AM является биссектрисой угла A1MD.
Таким образом, угол C1AA1 будет равен удвоенному углу A1MD.
Осталось только определить угол A1MD.
Так как AD || BC, то угол AMD является вертикальным (или соответственным) углом с углом ABC.
Известно, что прямоугольник ABCD, поэтому ABC = 90°.
Таким образом, угол AMD равен 90°.
Значит, угол A1MD равен 45°, а угол C1AA1 равен 2 * 45° = 90°.
Ответ: угол между прямыми MN и DD1 равен 90°, а угол между прямыми BB1 и A1C1 также равен 90°.