Андрей петрович взял кредит на несколько лет и выплачивает его равными ежегодными платежами по 2руб. при этом в начале каждого

Question

Математика: Андрей петрович взял кредит на несколько лет и выплачивает его равными ежегодными платежами по 2руб. при этом в начале каждого года сумма кредита увеличивалась на10%, а в конце года производился платёж. если бы андрей не делал платежей, то за это время вследствии начисления процентов сумма кредита составвила бы 928200 руб. на сколько лет был взят кредит? (полное решение)

denmalyshevs · Answer

Обозначим: S — сумма кредита, n — срок, на который взят кредит, a = 1,1 — число, при умножении на которое число увеличивается на 10%, x = 200000 — ежегодный платёж.

Если бы Андрей Петрович не делал платежей, сумма долга составила бы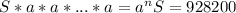 S*a*a*...*a=a^nS=928200 .

При совершении платежей остаток увеличивается на 10% (т. е. умножается на a), а затем из него вычитается ежегодный платёж, и так n раз: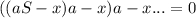 ((aS-x)a-x)a-x...=0 . Преобразуем левую часть:

$((aS-x)a-x)a-x...=a^nS-a^{n-1}x-a^{n-2}x-...-ax-x=\\=a^nS-x(a^{n-1}+a^{n-2}+...+a+1)=a^nS-x\frac{a^n-1}{a-1}$

Последнее преобразование следует из того, что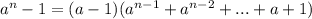 $a^n-1=(a-1)(a^{n-1}+a^{n-2}+...+a+1)$ .

Из полученных уравнений составим систему:

$\left \{ {{a^nS-x\frac{a^n-1}{a-1}=0} \atop {a^nS=928200}} \right. \Rightarrow 928200-200000*\frac{1.1^n-1}{1.1-1}=0\\200000*\frac{1.1^n-1}{0.1}=928200\\1.1^n-1=\frac{928200*0.1}{200000}=\frac{4641}{10000}\\(\frac{11}{10})^n=\frac{14641}{10000}=(\frac{11}{10})^4\\n=4$

ответ: на 4 года

Популярные вопросы