Алгебра, решить уравнения, 
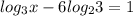
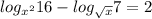
Другие вопросы по теме Математика
Популярные вопросы
- 25 ! нужно выбрать любой алкен и из него сделать превращение по ципочке...
2 - Определить напряжение на зажимах генератора параллельного возбуждения...
2 - Сыну и маме 40 лет. сыну и папе 42 года. а сыну, маме, папе вместе...
2 - Найдите координаты точек пересечения графиков функции: y=-0.5x^2+7,5...
3 - 3класс 2 часть ст 119 7 прочитай стихотворение константина льдова...
3 - Реши систему уравнений 4у-4х=-7 и 4у+х=2...
2 - Сделать дненик самоконтроля(самонаблюдений) по физкультуре сперва...
3 - Найти предел, , заранее заменой переменной...
3 - Какие события произошли в следующие годы xix века: 1. 1801 г. 2....
3 - Составить пословицы: 1коса-камень 2.лес - дрова 3.шило - мешок 4.язык...
3
log(3) x^2 - log(3) x/(x + 6) = 3
одз
x > 0
x/(x + 6) > 0 x < - 6 x > 0
x ∈ (0, +∞)
log(3) x^2 : x/(x + 6) = log(3) 3^3
log(3) x(x + 6) = log(3) 27
x^2 + 6x - 27 = 0
D = 36 + 4*27 = 144
x12 = (-6 +- 12)/2 = -9 3
x = -9 < 0 не корень
х = 3
log(3) x - 6log(2) 3 = 1
одз x > 0
log(3) x = 1 + log(2) 3^6
log(3) x = log(2) 2*3^6
x = 3^(log(2) 2*3^6)
log(x^2) 16 - log(√x) 7 = 2
одз x > 0 x ≠ 1 x ≠ - 1
x ∈ (0, 1) U (1, +∞)
1/2 log(x) 16 - 2 log(x) 7 = 2
log(x) 4 - log(x) 49 = log(x) x^2
log(x) 4/49 = log(x) x^2
x^2 = 4/49
x1 = -2/7 нет < 0
x2 = 2/7