ABCD - любой четырёхугольник I, J, K и L середины сторон AB, BC, CD, DA
Докажите, что вектор IJ = 1/2 вектор АС
Другие вопросы по теме Математика
Популярные вопросы
- Раскрой правильно скобки в предложения ...
2 - с 1 или 2 а желательно с двумя заданиями...
3 - 1. Фрагмент ДНК имеет 20%A. 16%T,8%Ц, 18%Г. Какой процентный состав А.Т.Ц.Г....
2 - Из 2 посёлков расстояние между которыми 78 км вышли Одновременно навстречу...
2 - 1 задание составить свой блог,типо такого как на фото...
1 - в ромбе АВСД : АД=20см, ВД=24см ,О-точка пересечения диагоналей .Найти...
2 - А.П. Чехов. Рассказ « Пересолил» От ответьте на вопросы:Какой рассказ «...
3 - 166.найдите сумму. а)4/9+2/9+1б)4/11+3+3/11в)1 5/12+1/12+1/12г)12+5/6+1/6167.найдите...
1 - Найди ошибки проверь Выполнив действия....
2 - лучший ответ қазақ әдебиеті 6класс Тест. Әдебиет пәні С.Мұратбеков «Жусан...
2
(в приложении рисунок)
Вот смотри. Мы начертили произвольный четырехугольник ABCD и отметили все точки, какие было нужно, а теперь будем рассматривать треугольник ABC и треугольник IBJ. Нам нужно доказать, что IJ=1/2AC, иначе говоря, оказать, что AC=2IJ. Что мы имеем? AI=IB, так как I - это середина AB; BJ=JC, так как J - это середина BC. Тогда AB=2BI, а BC=2BJ. Так же ΔABC и ΔIBJ имеют общий угол B, то есть ∠АВС=∠IBJ. И теперь мы видим что ΔABC и ΔIBJ подобны по второму признаку подобия треугольников, по двум сторонам и углу между ними (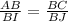 и ∠АВС=∠IBJ). Подобные треугольники - это треугольники, углы у которых соответственно равны, а стороны соответственно пропорциональны. В таком случае, все стороны пропорциональны
и ∠АВС=∠IBJ). Подобные треугольники - это треугольники, углы у которых соответственно равны, а стороны соответственно пропорциональны. В таком случае, все стороны пропорциональны 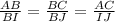 . Теперь найдем их пропорциональное соотношение:
. Теперь найдем их пропорциональное соотношение:
или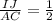 .
.
P.S. Вот и всё, надеюсь, понятно.