А) решите уравнение sin^2 x/2 - cos^2 x/2 = cos2x б) укажите корни уравнения , принадлежащие отрезку [ pi/2 ; 2pi ]
Другие вопросы по теме Математика
Популярные вопросы
- Расставьте знаки препинания и объясните их....
2 - ( ) С какими из перечисленных веществ будет реагировать гидроксид натрия:...
3 -  Мини сочинение на тему бактерии и грибы...
1 - Измерение прямоугольного параллелепипеда 15, 50, 36. Точки M, N и K...
3 - составить текст с этим словами: 1)купить билет 2)сесть 3)пропустить...
3 - 2 Как изменится уровень ртути в трубке Торричелли при изменении атмосферного...
3 - 11. Complete the sentences with do, would, are or to. 1) Do you want...
3 - Найдите следующее число в последовательности: 4, 13, 26, 43, 64...
3 - Замени умножение сложением и вычесли. 31×2 42×2 13×3 9×3 8×5 23×3 25л×3...
2 - Выпиши из предложений словосочетания числительное + существительное,...
1
a)
б)
ответ : а)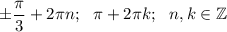
б)![\dfrac {5\pi}3\in\bigg[\dfrac {\pi}2;2\pi\bigg];~~\pi\in\bigg[\dfrac {\pi}2;2\pi\bigg]](/tpl/images/0571/0317/64de8.png)