Математика: А) Решите уравнение 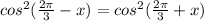б) Найдите все корни этого уравнения, принадлежащие промежутку [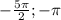]. , напишите подробное решение. Особенно не понятны тригонометрические преобразования.

А) Решите уравнение $cos^{2}(\frac{2\pi }{3}-x)=cos^{2}(\frac{2\pi }{3} +x)$ б) Найдите все корни этого уравнения, принадлежащие промежутку [ $-\frac{5\pi }{2} ; -\pi$ ].

, напишите подробное решение. Особенно не понятны тригонометрические преобразования.

Ответы

Fura44 18.04.2021 11:20

Применяем формулу разности квадратов, затем формулы суммы и разности косинусов, далее упрощаем, используя свойство чётности синуса и косинуса

$\cos^2{(\frac{2\pi}{3}-x)}=\cos^2{(\frac{2\pi}{3}+x)} \\ \\ \cos^2{(\frac{2\pi}{3}-x)}-\cos^2{(\frac{2\pi}{3}+x)}=0 \\ \\ (\cos{(\frac{2\pi}{3}-x)}-\cos{(\frac{2\pi}{3}+x)})\cdot (\cos{(\frac{2\pi}{3}-x)}+\cos{(\frac{2\pi}{3}+x)})=0 \\ \\ (-2\cdot \sin{(\frac{(\frac{2\pi}{3}-x)-(\frac{2\pi}{3}+x)}{2})}\cdot \sin{(\frac{(\frac{2\pi}{3}-x)+(\frac{2\pi}{3}+x)}{2} )})\cdot (2\cdot \cos{ (\frac{(\frac{2\pi}{3}-x)+(\frac{2\pi}{3}+x) }{2})\cdot \cos{ (\frac{(\frac{2\pi}{3}-x)-(\frac{2\pi}{3}+x)}{2})}}){=0}$

$-4 \sin{(\frac{-2x}{2})}\cdot\sin{(\frac{\frac{4\pi}{3}}{2})}\cdot \cos{ (\frac{\frac{4\pi}{3}}{2}) }\cdot \cos{(\frac{-2x}{2})}=0 \\ \\ -4\cdot \sin{(-x)}\cdot \sin{(\frac{4\pi}{6})}\cdot \cos{(\frac{4\pi}{6})}\cdot \cos{(-x)}=0 \\ \\ -4\cdot (-\sin{x})\cdot \sin{(\frac{2\pi}{3})}\cdot \cos{(\frac{2\pi}{3})}\cdot \cos{x}=0 \\ \\ 4\sin{x}\cdot \frac{\sqrt{3}}{2}\cdot (-\frac{1}{2})\cdot \cos{x}=0 \\ \\ -\sqrt{3}\cdot \sin{x}\cos{x}=0 \\ \\ \sin{x}=0; \ \ \ \ \ \cos{x}=0$

$x_1=\pi n, \ n \in Z; \ \ \ \ \ x_2=\frac{\pi}{2}+\pi n, \ n \in Z$

$x_1=\pi\cdot (-1)=-\pi \\ \\ x_2 =\pi \cdot (-2)=-2\pi \\ \\ x_3=\frac{\pi}{2}+\pi \cdot (-2) =\frac{\pi}{2}-2\pi=\frac{\pi-4\pi}{2}=-\frac{3\pi}{2} \\ \\ x_4=\frac{\pi}{2}+\pi \cdot (-3)=\frac{\pi}{2}-3\pi=\frac{\pi-6\pi}{2}=-\frac{5\pi}{2}$