A)Решить уравнение 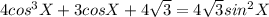 b)найти точки на промежутке [
b)найти точки на промежутке [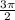 ; 3
; 3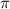 ]
]
Другие вопросы по теме Математика
Популярные вопросы
- Что будет если я сьем столовую ложку зубной пасты?отравление будет?...
2 - Розчинність KClO3 при 70°C — 30,2 а при 30°C — 10,1. Яка маса солі випала...
2 - Complete the gaps with possessive adjectives.what s your address? ...
1 - Доклад на тему Украина. В этом докладе должны быть 1 история народа 2 место...
2 - Взять научный факт (война, революция или открытие) и разложить на составляющие...
1 - 3. Основанием прямого параллелепипеда служит параллелограмм, стороны которого...
1 - Как изменялся объём изображений территории Земли и Донецкого края на географических...
1 - Три резистора з’єднані паралельно. Визначте R екв та намалюйте схему з’єднання,...
2 - 1.Выполнить всю грамматическую основу. 2.и обьяснить!почему там дееп и т.д.Текст:Вернувшись...
3 - Тіло рухається прямолінійно зі швидкістю v(t)=8+0,2t (м/с). Знайдіть шлях...
3
n€Z
€ читать "принадлежит"
б).
х=1,5π
х=2,5π
х=(2 5/6)π
Пошаговое объяснение:
cosx=0 честный случай
n €Z
n €Z
во вложении два фото