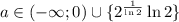A log2(|x-2|)=|x-2| при каком значение параметра а у уравнения будет два ответа? уравнение с параметром
Другие вопросы по теме Математика
Популярные вопросы
- Найти площадь каждой из закрашенных частей на рисунке, если все...
3 - Вкаком предложении выделенное слово является прилагательным? 1....
2 - Чем похожи 15 летний капитан и артур грэй...
2 - Чем известен остров ! а)не живут птицы б)не живут никакие животные...
2 - Уявіть, що ви були очевидцем падіння і розграбування вічного міста...
3 - При рычага поднимают груз массой 150 кг на высоту 40 см. к другому...
2 - Определи расстояние от п.а до п.б,если по карте расстояние 8см,а...
3 - Розбір числівника 29,2 як частина мови. ...
1 - Построить график функции у=1/10х ^5-5/6х^3+2х...
2 - Номер 244 все действие умрляю...
1
Пошаговое объяснение:
Заметим, что уравнение симметрично относительно x = 2: если 2 + x₀ — решение уравнения, то и 2 - x₀ — решение уравнения. Значит, на промежутке x > 2 уравнение должно иметь ровно один корень, оно имеет вид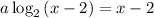 .
.
При a < 0 на промежутке x > 2 в левой части — монотонно убывающая функция, в правой части — монотонно возрастающая функция. Значит, уравнение имеет один корень, а исходное — два корня.
При a = 0 x - 2 = 0, x = 2, но x ≠ 2 по ОДЗ, корней нет.
При a > 0 слева и справа на промежутке x > 2 — монотонно возрастающие функции, при этом справа — прямая. Значит, чтобы был один корень, эта прямая должна быть касательной.
Производная функции левой части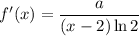 . Это коэффициент перед x, он равен 1 (касательная — y = 1·x - 2):
. Это коэффициент перед x, он равен 1 (касательная — y = 1·x - 2):
Подставим в исходное уравнение:
Таким образом,