A)докажите, что существует палиндром, кратный 2^3. b) докажите, что существует палиндром, кратный 6^10
Другие вопросы по теме Математика
Популярные вопросы
- Решите системой уравнений. подробно. сумма двух чисел равна 180,частное от...
1 - 14+y-2*3+4=20 дайте решение заранее !...
2 - Вдвух бочках было поровну воды. когда из первой бочки взяли 54 л, а из второй-6...
3 - Вовощехранилище заложили 17 ящиков с капустой по 9 кг в каждом и 8 одинаковых...
1 - Два класса убирают территорию школы 5 клас за 10 минут а 6 за 15 за какое...
2 - Вставить пропущенные буквы ,разобрать слова по составу : раздробил,разглядел,разъяснил,расплескал...
2 - Какое слово образовано приставочно-суффиксальным заметка 2-должностной 3-...
1 - Найдите координату середину отрезка,соединяющую точку: 1 и 7,3 и 8,2 1/4 и...
1 - 3) все киты являются млекопитающими. ни один кит не является сухопутным животным....
1 - Напишите, , сочинение на тему человек доброй души !...
2
а)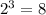 - а это уже палиндром
- а это уже палиндром
б) Сначала построим палиндром, кратный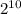
Пусть A - число из цифр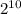 , записанных в обратном порядке (очевидно, что
, записанных в обратном порядке (очевидно, что 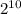 не оканчивается на 0 (иначе
не оканчивается на 0 (иначе 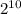 кратно 5), а значит A существует). Пусть также число цифр A равно n.
кратно 5), а значит A существует). Пусть также число цифр A равно n.
Тогда искомое число можно получить записав подряд число A, 10 нулей и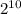 . И правда, это число равно
. И правда, это число равно 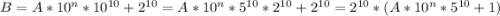 - кратно
- кратно 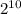
Записав 3 раза подряд число B, получим палиндром, кратный 3. И правда: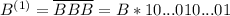 . Сумма цифр
. Сумма цифр 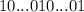 равна 3, а значит число кратно 3, а значит
равна 3, а значит число кратно 3, а значит 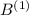 кратно
кратно 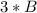 . Повторив эту операцию уже с числом
. Повторив эту операцию уже с числом 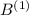 , получим
, получим 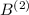 , кратное уже
, кратное уже  . Наконец на 10ом шаге получим палиндром
. Наконец на 10ом шаге получим палиндром 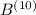 , кратный
, кратный 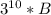 .
.
Т.к. B кратно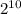 , то
, то 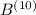 кратно
кратно  =
=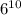
А значит палиндром, удовлетворяющий условию, существует.
Ч.т.д.