A²+4b²+9≥2ab-6b-3a
Довести нерівність! ДУЖЕ ПОТРІБНО!
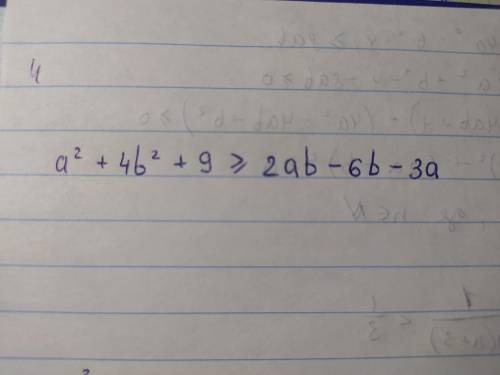
Другие вопросы по теме Математика
Популярные вопросы
- Вставьте относительные местоимения в придаточных определительных Предложениях....
3 - Придкмай свою ввдумпную небольшую историю...
1 - Кто сделает эту задачу от ...
2 - Https://teeveee.com/watch/oDZTcnSSVhVeD5r https://teeveee.com/watch/aLNxkPi5bIJLuNY...
1 - Практична робота 5 біологі...
1 - Письмо. Задание 2. Напишите репортаж.Объем слов 80 - 1001)Представьте,...
2 - по математике реши задачу лошадей 48 животных коров неизвестно в 6...
2 - У меня СОР по Историй Казахстана. ...
2 - Test 7-10 1. Match the words to form collocations 1. cut 2. lose 3....
1 - Геродоттын не басты максаты...
1
Нам нужно доказать, что A² + 4b² + 9 ≥ 2ab - 6b - 3a.
Для начала приведем все переменные в левой части неравенства:
A² + 4b² + 9 ≥ 2ab - 6b - 3a
Перепишем это неравенство в виде квадратного трехчлена:
A² + 4b² + 9 - 2ab + 6b + 3a ≥ 0
Теперь произведем алгебраические операции, чтобы упростить выражение:
A² - 2ab + 3a + 4b² + 6b + 9 ≥ 0
Теперь проведем группировку членов:
(A² - 2ab + 4b²) + (3a + 6b) + 9 ≥ 0
(A - b)² + 2(3a + 2b) + 9 ≥ 0
Теперь неравенство приняло вид суммы неотрицательных чисел, так как квадрат и произведение A - b всегда положительны.
Таким образом, неравенство доказано.
Если у вас есть дополнительные вопросы или что-то непонятно, не стесняйтесь задавать!