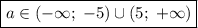(a-3)*4^x-8*6^x+(a+3)9^x= решить при каких значениях а уравнение не имеет корней
Другие вопросы по теме Математика
Популярные вопросы
- 1437 см2= дм2 см2 2415мм2= см2 мм2 46030 дм2= м2 дм2...
3 - Верно ли утверждение: если промышленность страны не может увеличить выпуск продукции,...
3 - Как разобрать по составу слово сказали...
3 - Какой объем раствора серной кислоты с концентрацией 60% мас ро= 1,5г/см^3 надо взять...
3 - Найти сочинение на тему: нужны ли каникулы 4 кл...
2 - Представь каждое из чисел 25,81,100,169,289,361 в виде произведения двух одинаковых...
3 - При силе тока в катушке 1.5 а энергия магнитного поля равна 0.45 дж. найдите индуктивность...
1 - Уровнения: 528: k-24=64; p: 38-76=38; 43m-215=473решите...
3 - Отрезок, равный 26 см. разделён на три неравных отрезка. длина среднего отрезка...
2 - Sin(π/2+а)=-1/2 п3п/2 найти sin(30+а)...
1
Для удобства произведём замену переменных:
Рассмотрим последнее уравнение как квадратное в отношении переменной p (можно и в отношении q - результат будет тот же). Оно не будет иметь корней, если его дискриминант будет отрицательным.
Решение задачи сводится к решению неравенства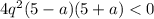 . Очевидно, что множитель 4q² будет положительным при любых q≠0. Однако ранее мы определили, что q>0, значит этот множитель не влияет на неравенство, и мы можем его отбросить.
. Очевидно, что множитель 4q² будет положительным при любых q≠0. Однако ранее мы определили, что q>0, значит этот множитель не влияет на неравенство, и мы можем его отбросить.
Получаем три интервала для a: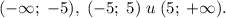
Проверив знаки на каждом интервале, получим, что последнее неравенство выполняется при