А) (1/5)^3-2x =125
Б) log4(x^2 - 15x)=2
В) 3cos 2x - 5 sin x +1=0
Другие вопросы по теме Математика
Популярные вопросы
- Доказать что /_\ABC =/_\ДСЕ Найти стороны /_\ АBE, если ДЕ = 3см, ДС=...
1 - 1) x+x2 +x3 2)(3 – a)2 +5(3- a) 3) 162²bc? +24abc...
1 - Как вы думаете, почему из такого большого количества претендентов, выбор...
1 - решить уравнения: а) 4 4/9:x=5/27; б) (x+1,3)•1 4/9=5,2 ( )...
2 - Әдеби тіл нормалары Еліктеу сөздердің түрлерін қатыстырь сұхбат құрастырыңдар...
2 - Задание 1. В таблице даны некоторые виды прикладного искусства древните...
3 - По дроту тече електричний струм. Визначте як зорієнтується магнітна стрілка,...
3 - сделайте найдите слова приставочные суффиксальный и сложение...
2 - 4. Кто из персонажей дружил с Чацким? Платон Михайлович Репетилов Загорецкий...
1 - сделать я буду очень благодарен...
2
№1.
ответ: -1 и 16
Пусть sin x = t, |t|≤1 , тогда
Вернёмся к замене:
ответ: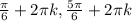 , k∈Z
, k∈Z