А) (1 + 1/11) × ( 1 + 1/12) × (1 + 1/13) × ... × (1 + 1/19)= б) (1 + 1/21) × (1 + 1/22) × (1 + 1/23) × ... × (1 + 1/29) =
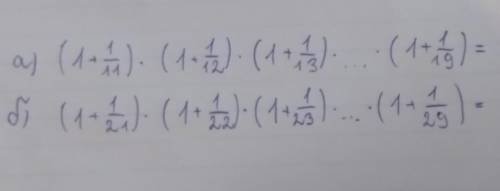
Другие вопросы по теме Математика
Популярные вопросы
- Задание 4 (2) а) На рисунке показано орбитальное вращение Земли вокруг Солнца....
1 - ответь на вопросы часовая стрелка находиться между 3 и 4 делениями, а минутная...
2 - подстановки 3x-2y=44x+y=-6...
1 - Елементи конструкції велосепеда що впливає на безпеку руху...
3 - 1) новости, которые изменили мир, не имеют значения для будущего? 2) какие новости...
1 - 1. The main idea of the story is: * a. there are many ways to travelb. airplanes...
3 - 2.Туған елімізді суреттеп, «Қазақстан – сахатшылар көзімен» тақырыбында эссе...
2 - Оцінити значення виразу a)x+y , б)х-у, в)ху, якщо 2 х ,5, 4 у 7...
1 - 2. Дополни предложения. Колебание воздуха, распространяющееся в виде волн, этоЧем...
1 - Ғұнардың монғол тілдес шығыстағы көршіс?...
1
ответ
Пошаговое объяснение: