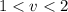9 класс решить , как видите не зажал
Другие вопросы по теме Математика
Популярные вопросы
- РЕШИТЬ ЗАДАЧА И СДЕЛАТЬ УСЛОВИЕ ЗАДАЧИ:ширина земельного участка 36 метров,...
3 - Решите уравнения:. А)(60•а-32):16=13. Б)75-960:(b+39)=55...
2 - Які моральні ціності в романі джим гудзик і машинист лукас поже...
3 - Запиши характеристику одной из форм поверхности Земли...
2 - 2. Есептің берілуін қысқаша жаз. Оны амалдар бойыншашығар.«Бөбек» лагерінде...
3 - Разложите на множители 3(х-27)...
2 - Реши систему уравнений: {2x+10y=254x−5y=3...
1 - Выявите особенности сезонных кочевок: кыстау, коктеу, жайляу и кузеу, заполните...
2 - Спишите, вставляя пропущенные буквы и расставляя знаки препинания. Как кр..сивы...
2 - Все оксиды основные в ряду:а) K2O, CO2, CrO3, P2O5б) SiO2, SO3, CrO, Cr2O3в)...
3
ответ: 1 < v < 2
Пошаговое объяснение:
Для существования подкоренного выражения необходимо выполнение условия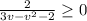 и для дроби знаменатель не должен быть равным 0:
и для дроби знаменатель не должен быть равным 0: 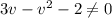
Два этих условия можно объединить в одно: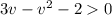
решим это неравенство с теоремы Виета:
Применив метод интервалов находим