843. При каких значениях переменной х обращается в верное числовое равенство уравнение:
1) 10 - x x -8;
2) 21 + х= 6;
3)4-5х=0
4)0,5х+20,1=0,1
5)
6)
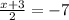
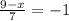
Другие вопросы по теме Математика
Популярные вопросы
- :сделайте заперечну форму к реченню they travelled to france...
3 - Начертить непрямой угол с вершиной в точке а.на одной стороне...
1 - Разложите на множители а) 3х+12уб)2а^5+а^3в)4х+16уг)3а^2+азаранее...
3 - Провідміняйте 2 числівника: тридцять шостою і сімдесят восьма....
3 - (5,7разделить 0,3минус 8 1/3) умножить на 0,75/ ///(2 1/8 плюс...
3 - 30 . сделайте полный синтаксический разбор предложения, и подчеркните...
2 - Разложите многочлены на множители с формул сокращённого умножения....
2 - Как на будет выражение: извините, я вас не понял?...
1 - Разложите на множители : ! 2x+6+x^2+3x ^2-это степень. в интернете...
2 - На какое число надо разделить 1000 чтобы получилось 2?...
1
1) 10 - x x - 8:
Для решения этого уравнения, нам нужно раскрыть скобки, а затем сгруппировать все слагаемые с переменной x влево, а все константы - вправо.
Решение:
10 - x x - 8 = 0
10 - 2x - 8 = 0 (раскрыли скобки)
2 - 2x = 0 (сократили)
2 = 2x (прибавили 2x)
x = 1 (разделили на 2)
2) 21 + х = 6:
Для решения этого уравнения, мы должны избавиться от константы 21, перенося ее вправо, и от переменной х, перенося ее влево.
Решение:
21 + x = 6
x = 6 - 21 (вычли 21 из обеих сторон)
x = -15
3) 4 - 5х = 0:
Для решения этого уравнения, мы должны перенести все слагаемые с переменной x влево, а константу 4 - вправо.
Решение:
4 - 5x = 0
-5x = -4 (прибавили 4 к обоим сторонам)
x = -4 / -5 (разделили на -5)
x = 4/5
4) 0,5х + 20,1 = 0,1:
Чтобы решить это уравнение, мы должны перенести константу 20,1 вправо, а все слагаемые с переменной x влево.
Решение:
0,5x + 20,1 = 0,1
0,5x = 0,1 - 20,1 (вычли 20,1 из обеих сторон)
0,5x = -20 (сократили)
x = -20 / 0,5 (разделили на 0,5)
x = -40
5)
Чтобы решить это уравнение, мы должны умножить обе стороны на 2, чтобы избавиться от знаменателя.
Решение:
2 * (x + 3) = -7 * 2 (умножили обе стороны на 2)
2x + 6 = -14 (произвели умножение)
2x = -14 - 6 (вычли 6 из обеих сторон)
2x = -20 (сократили)
x = -20 / 2 (разделили на 2)
x = -10
6)
Чтобы решить это уравнение, мы должны умножить обе стороны на 7, чтобы избавиться от знаменателя.
Решение:
7 * (9 - x) = -1 * 7 (умножили обе стороны на 7)
63 - 7x = -7 (произвели умножение)
-7x = -7 - 63 (вычли 63 из обеих сторон)
-7x = -70 (сократили)
x = -70 / -7 (разделили на -7)
x = 10
Таким образом, значения переменной x, при которых уравнения становятся верными числовыми равенствами:
1) x = 1
2) x = -15
3) x = 4/5
4) x = -40
5) x = -10
6) x = 10