84. (03-9-9) Упростите а + 2а + За + ... +na + па n2 - 2n - 3 ab 2(Vaь - b) ab а - 6 За 2а A)a + n B) 2(n - 3) 3n E)n – а (Vaь — atſat Am с) з(а + 1) D) ) n - 3
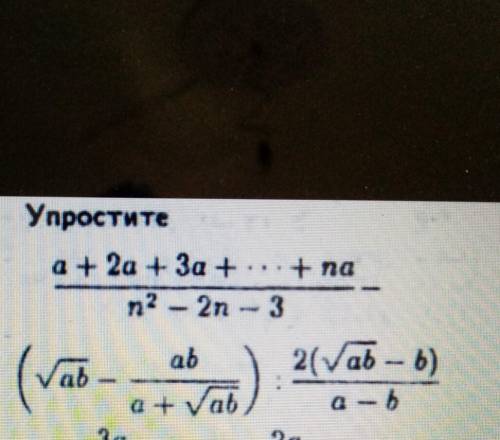
Другие вопросы по теме Математика
Популярные вопросы
- Прочитайте, объясните орфограммы на месте пропуска букв. 1. У Пети...
1 - Прочитайте загадку. Отгадайте. Найдите восклицательное предложение....
3 - Образуйте от данных слов имена прилагательные. Робок — робкий, сладок,...
2 - Распределите слова в четыре группы по орфограммам. Запишите. Л..сник,...
3 - От данных глаголов образуйте существительные с суффиксом -к-. Запишите....
1 - Разделите слова на две группы. Запишите. Город, шапка, провод, трубка,...
1 - Спишите загадку. Напишите отгадку. Он развесил в лесу свои сети....
3 - Образуйте однокоренные слова с суффиксом -к-. Лапа — лапка, борода,...
1 - Прочитайте. Подули с..рдитые ветры. Сне.. вып..дал и таял. Речка...
3 - К данным прилагательным подберите прилагательные-антонимы. Запишите....
2
1. Для начала рассмотрим члены выражения а + 2а + За + ... + na. Заметим, что эти члены представляют собой арифметическую прогрессию с разностью а, а первый член равен a. Для нахождения суммы арифметической прогрессии мы можем использовать формулу суммы прогрессии:
Sn = (n/2) * (2a + (n-1)d),
где Sn - сумма прогрессии, n - количество членов, а d - разность прогрессии.
Применяя эту формулу, получим:
а + 2а + За + ... + na = (n/2) * (a + na).
2. После этого рассмотрим следующий член в выражении n^2 - 2n. Мы можем разложить его на два члена: n^2 и -2n.
3. Затем рассмотрим последний член -3ab(Vaь - b)ab а - 6 За. Мы можем разложить его на несколько членов:
-3ab * (Vaь - b) = -3abVaь + 3ab^2,
-6 За = -6az.
4. Теперь объединим все полученные члены:
(n/2) * (a + na) + n^2 - 2n - 3abVaь + 3ab^2 - 6az.
5. Давайте упростим полученное выражение. Раскроем скобки:
(n/2) * a + (n/2) * na + n^2 - 2n - 3abVaь + 3ab^2 - 6az.
6. Вынесем общие множители:
n/2 * a + n^2/2 + n/2 * a^2 - n - 3abVaь + 3ab^2 - 6az.
7. Переупорядочим члены:
n/2 * a + n/2 * a^2 - 3abVaь + 3ab^2 - 6az + n^2/2 - n.
8. Объединим подобные члены:
n/2 * (a + a^2) - 3abVaь + 3ab^2 - 6az + n^2/2 - n.
Таким образом, упрощенное выражение равно:
n/2 * (a + a^2) - 3abVaь + 3ab^2 - 6az + n^2/2 - n.
Ответ: D) n/2 * (a + a^2) - 3abVaь + 3ab^2 - 6az + n^2/2 - n.