1. Математика
  2. 8. Решите уравнение

8. Решите уравнение \sin( \frac{\pi}{18} )x = - \frac{ \sqrt{3} }{2}
ответе укажите наименьший положительный корень уравнения. ответ:24

katyakhmel200 katyakhmel200    1   24.08.2021 19:30    0

Ответы
никуля40 никуля40  24.08.2021 19:40
Вот ответ! Я сокращённо сделала, могу подробно
8. Решите уравнение 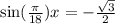ответе укажите наименьший положительный корень уравнения. ответ:24​
ПОКАЗАТЬ ОТВЕТЫ
Влад1488228 Влад1488228  24.08.2021 19:40

24

Пошаговое объяснение:

Чтобы получился показанный ответ нужно небольшое изменение условия. Вместо

sin(\frac{\pi }{18})x=-\frac{\sqrt{3} }{2}  

должно быть

sin(\frac{\pi }{18} x)=-\frac{\sqrt{3} }{2}

sin(\frac{\pi }{18} x)=-\frac{\sqrt{3} }{2}\\\frac{\pi }{18} x=(-1)^{k}*arcsin(-\frac{\sqrt{3} }{2})+k\pi=(-1)^{k+1}*arcsin\frac{\sqrt{3} }{2}+k\pi=(-1)^{k+1}*\frac{\pi}{3}+k\pi\\\frac{\pi }{18} x=(-1)^{k+1}*\frac{\pi}{3}+k\pi\\x=(-1)^{k+1}*6+18k\\x0; x=24; 30; 60; 66;...\\x_{min} =24

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
69devil69 69devil69  16.02.2022 08:48
І ВАРІАНТ Винести спільний множник за дужки: 15cb + 5bd=. б) 5b3c + d); B) 5bcd; 10. а) 15b(c+d); г) 5b5c + d)....
SmokeSivunenko SmokeSivunenko  16.02.2022 08:48
Найди значение выраженияx2+ 2 x3–√+ 6, еслиx =3–√+ 1....
Mariapolitova Mariapolitova  16.02.2022 08:49
7. На координатной прямой отмечены числа а и с (см. рис. 14). а с Рис. 14 Қакое из приведённых ниже неравенств для этих чисел неверно? 1)с+ 25 a+ 20 2)с- 12 a - 13...
AAndrey7600 AAndrey7600  16.02.2022 08:52
Линейное неравенство с одной переменной. Решение линейных неравенств с одной переменной. Урок 3 Реши неравенство. ответ: q ∈ ; . Назад Проверить...
gushagusha gushagusha  16.02.2022 08:53
7 вариант R а Правильный четырехугольник вписан в окружность. Найти неизвестные элементы....
помогите1178 помогите1178  16.02.2022 08:54
Дайте ответы. | :(...
Hafs Hafs  16.02.2022 08:56
Готовимся к изучению о новой темы 1. Используя действие сложения, проверьте, ве тание: 2) 11 11 3 24 8 - 1 12 1) 13,62 - 4,12 = 9,5; Задача от мудрой совы...
bojkovnikita bojkovnikita  16.02.2022 08:59
6. Впиши подходящий признак в общую часть диаграммы Венна. В какой части диаграммы будут фигуры? Соедини линиями. Фигуры, у которых Количество вершин больше 5-ти Фигуры,...
Rustem1112 Rustem1112  16.02.2022 09:00
Разложи число по разрядам: 2,738...
khfozilzhonov khfozilzhonov  16.02.2022 09:00
Решите задачу.Сторона квадрата равна 19,33см.Найди периметр...

Популярные вопросы