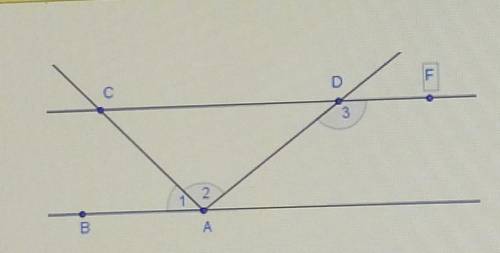
8. На рисунке СF||ВА, угол 1= углу 2, угол 3=140°. Найдите угол АСF​

Чтобы решить эту задачу, мы должны использовать свойства параллельных линий и углов.

У нас дано, что СF || ВА, что означает, что линия СF параллельна линии ВА. Также дано, что угол 1 равен углу 2, что можно обозначить как ∠1 = ∠2. И наконец, угол 3 равен 140°, что означает ∠3 = 140°.

Согласно свойству, если две параллельные линии пересекаются горизонтальной линией, то у соответствующих углов равны. Таким образом, ∠1 = ∠САС, и поэтому ∠САС = ∠2.

Мы также знаем, что сумма углов треугольника равна 180°. Таким образом, ∠ABC + ∠ВАС + ∠САВ = 180°. Мы можем подставить известные значения: угол 3 = ∠САВ = 140°. После подстановки получаем: ∠ABC + ∠ВАС + 140° = 180°.

Теперь мы можем выразить ∠ABC и ∠ВАС через известные значения:
∠ABC + ∠ВАС = 180° - 140°
∠ABC + ∠ВАС = 40°

Также мы знаем, что угол 1 равен углу 2, поэтому ∠ABC = ∠ВАС = ∠1 = ∠2.

Для решения этого уравнения нам нужно разделить данный угол на две части, чтобы найти его меру. Поскольку у нас два одинаковых угла, мы можем разделить 40° пополам, чтобы найти каждый угол: ∠ABC = ∠ВАС = 40° ÷ 2 = 20°.

Таким образом, угол АСF равен 20°.