794.теңдеулі шешіп түбірін табыңдар
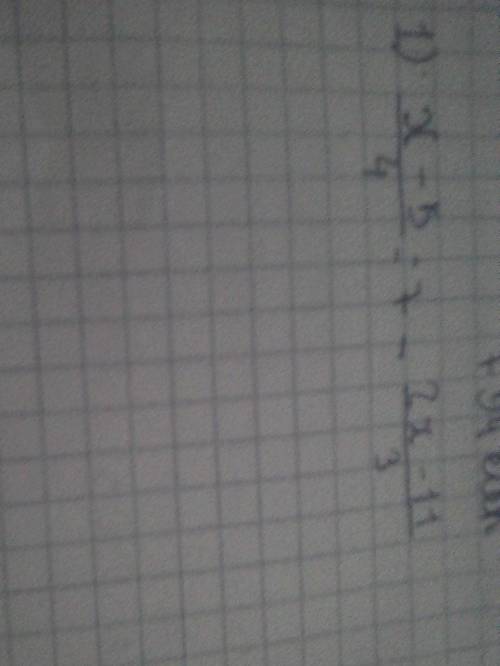
Другие вопросы по теме Математика
Популярные вопросы
- решить задачи с решением и правильно...
1 - 1) Складіть молекулярні рівняння реакцій, за до яких можна здійснити...
2 - Контрольная работа по родному (русскому) языку для 8 класса 1....
2 - Напишіть формули таких речовин та встановіть їх зв язки між собою...
1 - На сколько лет раньше Великой Французской буржуазной революции...
1 - Почему в начале произведения М. Ю. Лермонтова Иван Васильевичсравнивается...
1 - Найти сумму слагаемых 3n, где n – четное, кратное 3 целое число...
1 - Последовательность задана формулой an=2n+1 a) запишите пять первых...
1 - Можете написать формулу MIA...
3 - решить тригонометрическое уравнение, желательно с пояснениями....
2
На рисунке указаны числа в кругах, соответствующие каждой зубчатой шестерне. Если мы посмотрим на две соседние шестерни, то заметим, что каждая шестерня имеет разное количество зубьев.
Нам нужно найти "такую шестерню, клеточка под которой оказалась бы пустой". Для этого нам необходимо определить количество шестерней и число зубьев каждой шестерни в данной последовательности.
Если мы проанализируем последовательность, то заметим, что первая шестерня с 10 зубьями передается своим зубьям ровно половиной числа зубьев следующей шестерни. То есть, если первая шестерня имеет N зубьев, то вторая шестерня будет иметь N/2 зубьев.
Аналогично, вторая шестерня передает свои зубья третьей шестерне в количестве, равном половине зубьев второй шестерни. То есть, третья шестерня будет иметь N/2 * 1/2 = N/4 зубьев.
Этот процесс повторяется для каждой следующей шестерни, каждая из которых будет иметь наполовину меньше зубьев, чем предыдущая.
Найдем количество зубьев в каждой шестерне:
- Первая шестерня имеет 10 зубьев.
- Вторая шестерня имеет 10/2 = 5 зубьев.
- Третья шестерня имеет 5/2 = 2.5 зубьев.
На данном этапе происходит изменение конфигурации шестерней. Чтобы на этом этапе сохранить целое число зубьев, нам необходимо удвоить количество зубьев в первой шестерне, а затем принять половину зубьев как окончательное значение. Итак, для третьей шестерни у нас есть 2.5 зуба. Удвоим это значение: 2.5 * 2 = 5 зубьев. Затем возьмем половину этого значения: 5/2 = 2.5 зубьев.
- Четвертая шестерня имеет 2.5 * 2 = 5 зубьев.
- Пятая шестерня имеет 5/2 = 2.5 зубьев.
- Шестая шестерня имеет 2.5 * 2 = 5 зубьев.
- Седьмая шестерня имеет 5/2 = 2.5 зубьев.
- Восьмая шестерня имеет 2.5 * 2 = 5 зубьев.
Таким образом, восьмая шестерня имеет пустую клеточку под собой. Ответ на задачу: "Восьмая шестерня имеет пустую клеточку под собой".