1. Математика
  2. 70 б. ищу с решением

70 б. ищу с решением уравнения! найти общий интеграл однородного дифференциального уравнения первогопорядка

Inosya Inosya    2   26.06.2019 10:10    0

Ответы
кукипро кукипро  21.07.2020 09:27

Первый

Так как диф. уравнение однородное, то для него осуществляется замена y = ux, тогда y' = u'x + u, имеем:

u'x+u=3u+4~~~\Rightarrow~~~ u'x=2u+2~~~\Rightarrow~~~ \displaystyle \int\dfrac{du}{u+1}=\int \dfrac{2dx}{x}\\ \\ \\ \ln|u+1|=\ln |x^2|+\ln C~~~\Rightarrow~~~ u+1=Cx^2~~~\Rightarrow~~~ u=Cx^2-1

Выполнив обратную замену u = y/x, имеем:

\dfrac{y}{x}=Cx^2-1~~~~\Rightarrow~~~~\boxed{\dfrac{y}{x^3}+\dfrac{1}{x^2}=C}

Получили общий интеграл.

Второй

y'-\dfrac{3y}{x}=4

Умножим левую и правую части уравнения на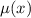 \mu (x), которое определяется соотношением:

\displaystyle \mu (x)=e^{\int-\frac{3}{x}dx}=e^{-3\ln |x|}=\dfrac{1}{x^3}

\dfrac{y'}{x^3}-\dfrac{3y}{x^4}=\dfrac{4}{x^3}\\ \\ y'\cdot \dfrac{1}{x^3}+y\cdot \left(\dfrac{1}{x^3}\right)'=\dfrac{4}{x^3}~~~~\Rightarrow~~~ \left(y\cdot\dfrac{1}{x^3}\right)'=\dfrac{4}{x^3}

Проинтегрируем обе части уравнения

\dfrac{y}{x^3}=\displaystyle \int\dfrac{4}{x^3}dx~~~~\Rightarrow~~~ \dfrac{y}{x^3}=-\dfrac{2}{x^2}+C~~~~\Rightarrow~~~ \boxed{y=Cx^3-2x}

Получили общее решение.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Creeper77 Creeper77  09.08.2019 17:50
Розставте 6 точок на 4 прямих так щоб на кожній було по 3 точки...
kirill1s kirill1s  09.08.2019 17:50
Найти число,которое на столько же меньше 5/12,на сколько 2/9 меньше 1/3 5 ,!...
likonady likonady  09.08.2019 17:50
Бақта екі жүйек құлпынай отырғызды . бірінші жүйектегі түп саны екінші жүйекке қарағанда 3 есе кем. бірінші жүйекке тағы да 14 түп отырғызылды. егер барлығы 118 түп болатын болса...
Zhaksyldi Zhaksyldi  09.08.2019 17:50
Перед вами одна из первых карт марса, выполненная в 19 веке и оказавшая огромное влияние на и дажекинематограф . на этой карте автором указаны проливы . при переводе этот термин...
Ozeplay Ozeplay  09.08.2019 17:50
Сколько будет 3 целых 7\25+2 целых18\25...
vadimplay2017 vadimplay2017  09.08.2019 17:50
Наруйте треуголник и на нём нарисуйте три медианы,три биссектрисы и три высоты(находить я вас ничего не...
uhudongoair uhudongoair  09.08.2019 17:50
Решить .в магазин 3т арбузов.в первый день продали 900 кг,во второй в два раза больше, чем в первый,а в третий день остальные. сколько килограммов арбузов продалиив третий день?...
Maksgeem Maksgeem  09.08.2019 17:50
Расстояние между двумя пристанями 60км.это расстояние лодка проплывает по течению реки за 4 ч.а против течения реки за 5ч.найдите собственную скорость лодки и скорость течения реки.составить...
seregaushakov13 seregaushakov13  09.08.2019 17:50
Составьте пример: 1) какое-то число : 100 * 40= ? 2) какое-то число - ? = ? 3) какое-то число: 100 * 25 = ? 4) т.д...
Tasha00000007 Tasha00000007  09.08.2019 17:50
Примеры чс техногенного характера в республике башкортостан...

Популярные вопросы