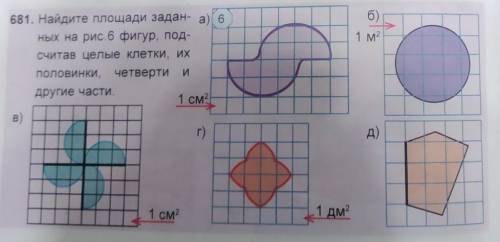
681. Найдите площади заданных на рис.6 фигур, подсчитав целые клетки, их половинки, четверти и
другие части.
надо найти площадь всех фигур

681. Найдите площади заданных на рис.6 фигур, подсчитав целые клетки, их половинки, четверти идругие

Ответы

Мила098 21.12.2023 05:03

Добрый день, давайте рассмотрим задачу и найдем площади каждой из фигур на рисунке.

1. Прямоугольник ABCD:
У прямоугольника две стороны, AB = 10 клеток и BC = 6 клеток.
Чтобы найти площадь прямоугольника, нужно перемножить длины его сторон: S = AB * BC = 10 * 6 = 60.
Площадь прямоугольника ABCD равна 60 квадратных клеток.

2. Квадрат EFGH:
Сторона квадрата EF = 4 клетки.
Площадь квадрата равна квадрату длины его стороны: S = EF^2 = 4^2 = 16.
Площадь квадрата EFGH равна 16 квадратным клеткам.

3. Прямоугольник IJKL:
У прямоугольника две стороны, IJ = 8 клеток и JK = 4 клетки.
Площадь прямоугольника равна произведению длин его сторон: S = IJ * JK = 8 * 4 = 32.
Площадь прямоугольника IJKL равна 32 квадратным клеткам.

4. Треугольник MNOP:
На рисунке задан равнобедренный треугольник, где MP = NO = 5 клеток, а длина основания MN = 6 клеток.
Чтобы найти площадь треугольника, нужно умножить длину основания на высоту и разделить полученное значение на 2: S = (MN * MP) / 2 = (6 * 5) / 2 = 15.
Площадь треугольника MNOP равна 15 квадратным клеткам.

5. Параллелограмм QRST:
У параллелограмма две стороны, QR = 4 клетки и RS = 3 клетки.
Чтобы найти площадь параллелограмма, нужно перемножить длину одной стороны на высоту, которая перпендикулярна этой стороне: S = QR × высота (H).
На рисунке дана диагональ RT, которую можно использовать вместо высоты.
Так как RT перпендикулярна стороне QR и проходит через точку P, то мы можем измерить длину диагонали RT: RT = 5 клеток.
Площадь параллелограмма QRST равна произведению длины стороны на длину диагонали: S = QR * RT = 4 * 5 = 20.
Площадь параллелограмма QRST равна 20 квадратным клеткам.

Таким образом, мы нашли площади всех пяти фигур на рисунке. Прямоугольник ABCD имеет площадь 60 квадратных клеток, квадрат EFGH - 16 квадратных клеток, прямоугольник IJKL - 32 квадратных клетки, треугольник MNOP - 15 квадратных клеток, а параллелограмм QRST - 20 квадратных клеток.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика