6. Двузначное число можно записать так ab = 10a + b, где а - число деко число единиц. Используя данную информацию, составьте уравнение по следующему условию: «число 3х в 2 раза больше, чем x4
Другие вопросы по теме Математика
Популярные вопросы
- Во время каникул ион и мария посадили саженцы. ион посадил в...
3 - Как сократить потери продукции при уборке и хранении?...
2 - Живое, обобщение представление о дейстаительности, выражение...
3 - Как составить красворд к рассказу юрия коваля усы и поросята....
2 - Какие формы собственности, и какие виды хозяйств существуют...
2 - Как можно повысить производительность труда в сельском хозяйстве?...
3 - Доклад про порозитов 5 класс беология !...
3 - Напишете введение и заключение ( проблема каждый человек должен...
3 - Вдетский сад 12 килограммов конфет и 15 килограммов яблок. один...
1 - Как сельское хозяйство влияет на здоровье и уровень жизни россиян?...
1
Двузначное число можно записать в виде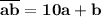 , где а и b - цифры , а - количество десятков , b - количество единиц .
, где а и b - цифры , а - количество десятков , b - количество единиц .
Над ab надо ставить черту, чтобы не путать обозначение числа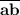 с произведением
с произведением 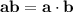 .
.
По условию число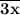 в 2 раза больше числа
в 2 раза больше числа 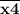 . Это можно записать так:
. Это можно записать так:
Такого быть не может, так как х - цифра, а не дробное число .