6) cos(2x + 4) = - cos 4x;
решите в скобках+п черта деления 4
Другие вопросы по теме Математика
Популярные вопросы
- Щоб знайти момент інерції твердого тіла відносно фіксованої осі...
3 - Мороз красный нос непонятные слова и их значения...
1 - КМАЛЯЮ СДЕЛАЙТЕ НОМЕР 3 все...
1 - Найдите значения выражений: 3 * 8 в кубе - 5 * 6 в кубе (5 в квадрате...
3 - Розгляньте хребет. З яких відділів він складається у: амфібіїрептиліїптахасссавця...
2 - Куда и зачем ехал Голован на корабле?Н.С. Лескова «Очарованный...
2 - Как сложилась дальнейшая судьба Ивана после выхода в отставку?...
2 - Куда и зачем ехал Голован на корабле?Н.С. Лескова «Очарованный...
2 - Задание 6. Образуйте степени сравнения от следующих имен прилагательных:...
3 - Задание 10. Исправьте лексические ошибки в предложениях. 1. Каникулы...
1
Используя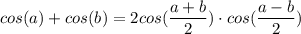 , преобразуем наше выражение
, преобразуем наше выражение
Рассмотрим все возможные случаи
1)
2)
Находим объединение и получаем результат