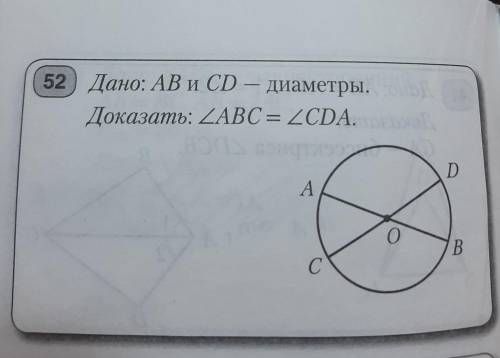
52) Дано: AB и CD — диаметры. Доказать: угол ABC = угол CDA.
Другие вопросы по теме Математика
Популярные вопросы
- Краплі якого короля дід Бочонок-аптекар обіцяв приготувати хворому...
3 - Рефлексия « Бір минуттык эссе » Мені таңғалдырды ... Мен үшін...
2 - Современные верстаки оснащены выдвижными ящиками для хранения...
2 - Охарактеризуйте досягнення та перспективи країн Африканського...
3 - По окончании футбольного турнира были названы 11 лучших футболистов....
1 - ТОЛЬКО НА 4,5 нужны хорошие оценки...
3 - Русский язык т.г Рамазанова 3 класс стр 445 упражнения 342 сделать...
3 - Упр 2 стр 70 - письменно ответы на вопросы: 1. What does Jessie...
2 - План урока литературы № 3 Тема: Путешествие Герды в поисках брата...
1 - не могу понять как делать? Дайте ответы...
3
Пошаговое объяснение:
Соединим СD и АD
Рассмотрим тр-ки АОD и СОВ
АО=ВО =АВ/2 как радиусы
СО=DO=CD/2 как радиусы
<АОD=<COB - как вертикальные
Тр-ки равны по 2 сторонам и углу между ними ( по 1 признаку)
В равных тр-ках соответственные элементы равны.
AO=BO=CO=DO значит тр-ки АОD и СОВ - равнобедренные и углы при основании равны:
<ОСВ=<ОВС=<ОАD=<ODA,
<ОDA=<CDA, <OBC=<ABC, отсюда
<АВС=<CDA
Или:
<АВС=<СDA - как вписанные углы,
опирающиеся на одну и ту же дугу АС:
Из теоремы о вписанном угле:
<АDC=1/2×<AOC
<ABC=1/2×<AOC,отсюда
<АВС=<АDC