5. Решите уравнение: (х2 + 5х – 6) (2х2 – 72)(х – 5) = 0.
Другие вопросы по теме Математика
Популярные вопросы
- На одній лісовій ділянці посадили 12 650 дерева на другій - у 5 раз...
3 - Вводу погружены три сплошных стальных шарика на нитях.на какой из них...
2 - Яку масову частку становить оксиген у складi калiй перманганату?...
1 - Твір мініатюра про свято пасхи 6-8 речень...
2 - Впалатку 84 кг гречневой крупы и 91 риса крупа каждого вида была расфасована...
3 - 5предложений на тему о природе см естоимениями...
2 - Представте трехчлен квадратом двухчлена 36х в квадрате+12х+1...
2 - 1. найдите массу фенола, полученного при действии 13,5г гидроксида натрия...
3 - По какому признаку можно объединитьданные слова в три группы. льдина.дождь.больница.деревья.медведь.альбом.здоровье.обезьяна.декабрь.коньки.играть.шалунья....
2 - Слова, пустые, что, без, орех. ядро...
3
Произведение равно нулю, когда хотя бы один из множителей равен нулю.
Решим каждое уравнение.
1)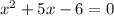
По теореме Виета:
2)
Не учитываем -6, потому что уже получили его в уравнении выше.
3)
Таким образом, данное уравнение имеет 4 корня.
ответ: -6; 1; 5; 6.