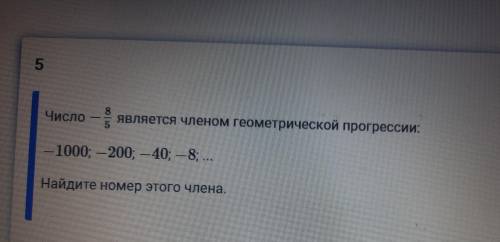
5 Число - является членом геометрической прогрессии: 8 -1000; -200; -40; -8; ... Найдите номер этого члена.

Для нахождения номера члена геометрической прогрессии нужно использовать формулу общего члена геометрической прогрессии:

aₙ = a₁ * r^(n-1),

где aₙ - n-ый член геометрической прогрессии,
a₁ - первый член геометрической прогрессии,
r - знаменатель прогрессии,
n - номер члена прогрессии, который мы хотим найти.

Нам даны первый член геометрической прогрессии (a₁ = 8) и неизвестный член (aₙ).

Для начала найдем знаменатель прогрессии:

r = a₂ / a₁,

где a₂ - второй член геометрической прогрессии.

В нашем случае a₁ = 8 и a₂ = -1000:

r = -1000 / 8 = -125.

Теперь у нас есть значение знаменателя прогрессии (r = -125), и нам нужно найти номер члена прогрессии (n), для которого aₙ = 5.

Подставим известные значения в формулу общего члена геометрической прогрессии:

5 = 8 * (-125)^(n-1).

Сократим на 8:

5/8 = (-125)^(n-1).

Так как нам нужно подобрать целое значение n, левую и правую части уравнения можно представить в виде степени с одинаковым основанием:

(5/8) = ((-125)^(-1)) * (-125)^n.

Применим свойство степеней:

(5/8) = (-125)^(-1+n).

Для того чтобы избавиться от отрицательного показателя степени, возьмем обратное значение от обеих частей:

8/5 = (-125)^(1-n).

Теперь можно представить число 8/5 в виде десятичной дроби:

8/5 = 1.6.

Таким образом, получаем:

1.6 = (-125)^(1-n).

Мы хотим найти значение n, для которого 1.6 будет равно (-125) в некой степени. Возведем число -125 в различные степени и посмотрим, на какую получаем значение 1.6:

(-125)^0 = 1,
(-125)^1 = -125,
(-125)^2 = 15625,
(-125)^3 = -1953125,
(-125)^4 = 244140625,
(-125)^5 = -30517578125.

Мы можем видеть, что при степени n = 1 получаем значение -125, а при степени n = 2 получаем значение 15625. Значит, n будет находиться между 1 и 2.

Используя метод более точного приближения, можно решить данную задачу численно или графически.

Однако, учитывая, что это задание для школьника, можно предположить, что искомое значение находится между 1 и 2, но ближе к 1.

Если принять, что выражение (-125)^(1-n) = 1.6, то можем записать:

1.6 = (-125)^(1-n) = 1.

То есть, получили уравнение:

1 = 1.6.

Это уравнение не имеет решения для n. Получить точное значение номера члена прогрессии в данном случае невозможно.

Однако, можно сделать вывод, что 5 не является членом данной геометрической прогрессии.